Suppose a patient is given 1.55 mg of I-131, a beta emitter with a half-life of 8.0 days. Assuming that none of the I-131 is eliminated from the person's body in the first 4.0 hours of treatment, what is the exposure (in Ci) during those first four hours?
Ch.20 - Radioactivity and Nuclear Chemistry

Chapter 20, Problem 78a
Complete each nuclear equation and calculate the energy change (in J/mol of reactant) associated with each (Al-27 = 26.981538 amu, Am-241 = 241.056822 amu, He-4 = 4.002603 amu, Np-237 = 237.048166 amu, P-30 = 29.981801 amu, S-32 = 31.972071 amu, and Si-29 = 28.976495 amu).
a. 2713Al + 42He → 3015P + ____
 Verified step by step guidance
Verified step by step guidance1
Identify the missing product in the nuclear reaction. The sum of atomic numbers and mass numbers must be conserved. For the given reaction, \( ^{27}_{13}\text{Al} + ^{4}_{2}\text{He} \rightarrow ^{30}_{15}\text{P} + X \), solve for X.
Calculate the atomic number and mass number of the missing product. The atomic number should be \( 13 + 2 - 15 = 0 \) and the mass number should be \( 27 + 4 - 30 = 1 \). Therefore, the missing product is a neutron \( ^{1}_{0}\text{n} \).
Write the complete nuclear equation: \( ^{27}_{13}\text{Al} + ^{4}_{2}\text{He} \rightarrow ^{30}_{15}\text{P} + ^{1}_{0}\text{n} \).
Calculate the mass defect by finding the difference in mass between the reactants and products. Use the given atomic masses: \( \Delta m = (26.981538 + 4.002603) - (29.981801 + 1.008665) \) amu.
Convert the mass defect from amu to energy using Einstein's equation \( E = \Delta m \times c^2 \), where \( c \) is the speed of light \( 3.00 \times 10^8 \text{ m/s} \). Then, convert the energy from J to J/mol by multiplying by Avogadro's number \( 6.022 \times 10^{23} \text{ mol}^{-1} \).

Verified video answer for a similar problem:
This video solution was recommended by our tutors as helpful for the problem above.
Video duration:
6mWas this helpful?
Key Concepts
Here are the essential concepts you must grasp in order to answer the question correctly.
Nuclear Reactions
Nuclear reactions involve changes in an atom's nucleus and can result in the transformation of one element into another. These reactions are characterized by the conservation of mass and energy, where the total mass and energy before and after the reaction remain constant. Understanding the types of nuclear reactions, such as alpha decay, beta decay, and fusion, is essential for completing nuclear equations.
Recommended video:
Guided course

Nuclear Binding Energy
Mass-Energy Equivalence
Mass-energy equivalence, expressed by Einstein's equation E=mc², indicates that mass can be converted into energy and vice versa. In nuclear reactions, a small amount of mass is often lost and converted into energy, which can be calculated to determine the energy change associated with the reaction. This concept is crucial for calculating the energy change in nuclear equations.
Recommended video:
Guided course
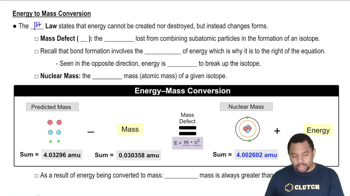
Energy to Mass Conversion
Atomic Mass Units (amu)
Atomic mass units (amu) are a standard unit of mass used to express atomic and molecular weights. The mass of an atom is often measured in amu, where 1 amu is defined as one twelfth of the mass of a carbon-12 atom. In nuclear equations, knowing the atomic masses of the reactants and products is vital for balancing the equation and calculating the energy change.
Recommended video:
Guided course

Atomic Mass
Related Practice
Textbook Question
Textbook Question
Complete each nuclear equation and calculate the energy change (in J/mol of reactant) associated with each (Be-9 = 9.012182 amu, Bi-209 = 208.980384 amu, He-4 = 4.002603 amu, Li-6 = 6.015122 amu, Ni-64 = 63.927969 amu, Rg-272 = 272.1535 amu, Ta-179 = 178.94593 amu, and W-179 = 178.94707 amu). a. _____ + 94Be → 63Li + 42He
Textbook Question
Write the nuclear equation for the most likely mode of decay for each unstable nuclide. a. Ru-114 c. Zn-58 d. Ne-31
Textbook Question
Write the nuclear equation for the most likely mode of decay for each unstable nuclide. b. Ra-216
