2. Graphs of Equations

Lines

2. Graphs of Equations

Lines

Struggling with College Algebra?

Join thousands of students who trust us to help them ace their exams!Watch the first video

Multiple Choice

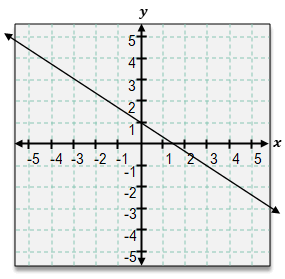
In the graph shown, identify the y–intercept & slope. Write the equation of this line in Slope-Intercept form.

$y=\frac23x+1$

$y=-\frac23x+1$

$y=-2x+1$

$y=x+2$

Verified step by step guidance

Identify the y-intercept of the line by locating the point where the line crosses the y-axis. In this graph, the line crosses the y-axis at y = 1.

Determine the slope of the line by selecting two points on the line. For example, choose the y-intercept (0, 1) and another point, such as (1, -1).

Calculate the slope using the formula: $ m = \frac{y_2 - y_1}{x_2 - x_1} $. Substitute the points (0, 1) and (1, -1) into the formula: $ m = \frac{-1 - 1}{1 - 0} = \frac{-2}{1} = -2 $.

Write the equation of the line in slope-intercept form, $ y = mx + b $, where m is the slope and b is the y-intercept. Substitute m = -2 and b = 1 into the equation: $ y = -2x + 1 $.

Verify the equation by checking that the line passes through the points used to calculate the slope. Substitute x = 0 and x = 1 into the equation $ y = -2x + 1 $ to ensure it yields the correct y-values (1 and -1, respectively).

6:49m

Watch next

Master The Slope of a Line with a bite sized video explanation from Patrick

Start learning

Lines practice set

Problem sets built by lead tutors

Expert video explanations

Go to Practice