Match the given polynomial function to its graph based on end behavior. f ( x ) = − 2 x 3 + x 2 + 1 f\left(x\right)=-2x^3+x^2+1 f ( x ) = − 2 x 3 + x 2 + 1

Hey, everyone. In this problem, we want to match the given polynomial function to its graph based on attend behavior. And here I have the function f of x is equal to negative 2x cubed plus x squared plus 1. So let's first determine what's going on with our end behavior by looking at that first term in standard form. Now, my function here is already written in standard form, so I can just go ahead and get started. So my very first term in standard form is this negative two x cube. So first, looking at my leading coefficient to determine what's going on on the right side, my leading coefficient is negative 2. Now because that leading coefficient is negative, my right side is going to fall down. So then determining what's going on on our ends, we're gonna take a look at our degree here, which in this case is 3. Now, 3 is an odd number. Remember, odd, opposite. So my n's are going to have the opposite behavior. So based on that, let's take a look at these graphs. I know that my right side should be falling down. So looking at the 3 graphs that I have here, it looks like in a, the right side is going up, so it is not a. And then in b, my right side is falling, so that could be an option. And then lastly, in c, my right side is also falling here, so we're between b and c. Let's consider what's going on on the ends. Now it said that our ends have the opposite behavior, so that means that my right side was falling, so my left side should be doing the opposite thing. Now looking at c here, my right side is falling, but my left side is also falling. That is not the opposite behavior so it is not c. And taking another look at b we said our right side was falling which is great and then our left side is rising, which is the opposite behavior. So our answer here is b. That's all for this one. Thanks for watching.

4. Polynomial Functions

Understanding Polynomial Functions

College Algebra

4. Polynomial Functions

Understanding Polynomial Functions

Struggling with College Algebra?

Join thousands of students who trust us to help them ace their exams!Watch the first video

Multiple Choice

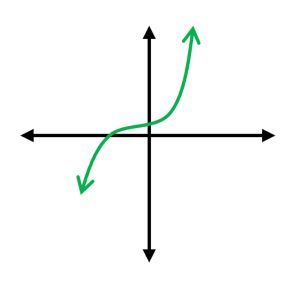
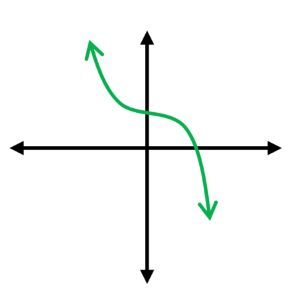
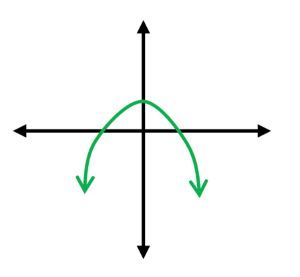
Match the given polynomial function to its graph based on end behavior. $f\left(x\right)=-2x^3+x^2+1$

A graphing coordinate with a curve

Verified step by step guidance

Identify the degree and leading coefficient of the polynomial function f(x) = -2x^3 + x^2 + 1. The degree is 3, and the leading coefficient is -2.

Determine the end behavior of the polynomial based on its degree and leading coefficient. Since the degree is odd (3) and the leading coefficient is negative (-2), the end behavior is: as x approaches positive infinity, f(x) approaches negative infinity, and as x approaches negative infinity, f(x) approaches positive infinity.

Analyze the graphs provided. Look for a graph where the left end (as x approaches negative infinity) goes up and the right end (as x approaches positive infinity) goes down.

Compare the end behavior of the polynomial with the end behavior of each graph. The graph that matches the end behavior of the polynomial is the correct one.

Select the graph that shows the correct end behavior: left end up and right end down, which corresponds to the polynomial f(x) = -2x^3 + x^2 + 1.

6:04m

Watch next

Master Introduction to Polynomial Functions with a bite sized video explanation from Patrick

Start learning

Understanding Polynomial Functions practice set

Problem sets built by lead tutors

Expert video explanations

Go to Practice

Struggling with College Algebra?

Match the given polynomial function to its graph based on end behavior. f(x)=−2x3+x2+1f\left(x\right)=-2x^3+x^2+1f(x)=−2x3+x2+1

Watch next

Understanding Polynomial Functions practice set

Match the given polynomial function to its graph based on end behavior. $f\left(x\right)=-2x^3+x^2+1$