Theory and Examples
In Exercises 51–54,
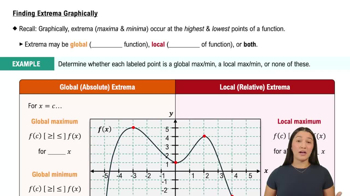
d. Over what intervals of x-values, if any, does the function y = f(x) increase as x increases? Decrease as x increases? How is this related to what you found in part (c)? (We will say more about this relationship in Section 4.3.)
y = −1/x