Theory and Examples
In Exercises 51–54,
c. For what values of x, if any, is f' positive? Zero? Negative?
y = −x²
 Verified step by step guidance
Verified step by step guidance Verified video answer for a similar problem:
Verified video answer for a similar problem: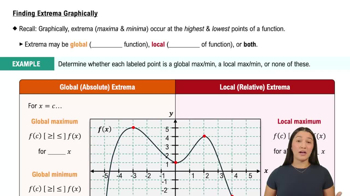



 5:58m
5:58mMaster Finding Extrema Graphically with a bite sized video explanation from Patrick
Start learning