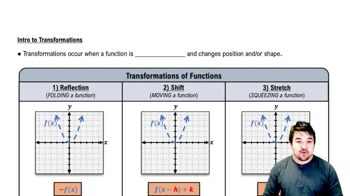
Shifting and Scaling Graphs
Suppose the graph of g is given. Write equations for the graphs that are obtained from the graph of g by shifting, scaling, or reflecting, as indicated.
f. Compress horizontally by a factor of 5
 Verified step by step guidance
Verified step by step guidance Verified video answer for a similar problem:
Verified video answer for a similar problem:

 5:25m
5:25mMaster Intro to Transformations with a bite sized video explanation from Patrick
Start learning