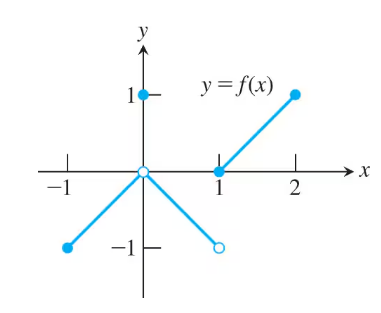
Average Rates of Change
In Exercises 1–6, find the average rate of change of the function over the given interval or intervals.
g(x)=x²−2x
a. [1, 3]
 Verified step by step guidance
Verified step by step guidance Verified video answer for a similar problem:
Verified video answer for a similar problem:


 6:47m
6:47mMaster Finding Limits Numerically and Graphically with a bite sized video explanation from Patrick
Start learning