Finding Deltas Graphically
In Exercises 7–14, use the graphs to find a δ>0 such that |f(x)−L| <ε whenever 0< |x−c| <δ.
 Verified step by step guidance
Verified step by step guidance Verified video answer for a similar problem:
Verified video answer for a similar problem: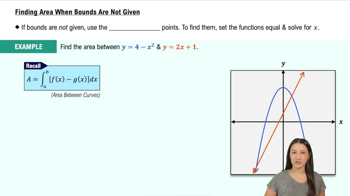

 6:47m
6:47mMaster Finding Limits Numerically and Graphically with a bite sized video explanation from Patrick
Start learning