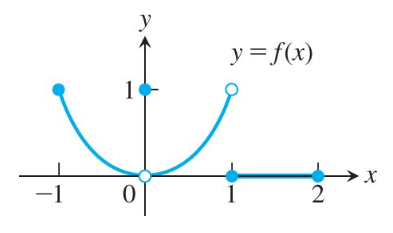
Finding Deltas Algebraically
Each of Exercises 15–30 gives a function f(x) and numbers L, c, and ε>0. In each case, find the largest open interval about c on which the inequality |f(x)−L| <ε holds. Then give a value for δ>0 such that for all x satisfying 0 < |x−c| < δ, the inequality |f(x)−L| < ε holds.
f(x) = 1/x, L = 1/4, c = 4, ε = 0.05