Here are the essential concepts you must grasp in order to answer the question correctly.
Limits at Infinity
Limits at infinity refer to the behavior of a function as the input approaches infinity. This concept is crucial in calculus for understanding how functions behave in extreme cases, particularly for rational functions, polynomials, and other expressions. Evaluating limits at infinity helps determine horizontal asymptotes and the end behavior of functions.
Recommended video:
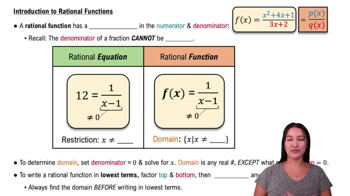
Rational Functions
A rational function is a function that can be expressed as the ratio of two polynomials. When analyzing limits at infinity for rational functions, the degrees of the numerator and denominator play a significant role in determining the limit. For instance, if the degree of the numerator is less than that of the denominator, the limit approaches zero as x approaches infinity.
Recommended video:
Intro to Rational Functions
Dominant Terms
In the context of limits, dominant terms are the terms in a polynomial or rational function that have the greatest impact on the function's value as x approaches infinity. For example, in the expression (3 + 10/x^2), as x becomes very large, the term 10/x^2 approaches zero, making the constant term 3 the dominant term. This concept is essential for simplifying expressions when calculating limits.
Recommended video:
Simplifying Trig Expressions Example 1
 Verified step by step guidance
Verified step by step guidance Verified video answer for a similar problem:
Verified video answer for a similar problem:


 6:47m
6:47m