Textbook Question
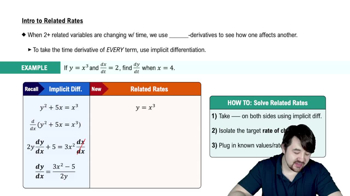
Draining a tank Water drains from the conical tank shown in the accompanying figure at the rate of 5 ft³/min.
a. What is the relation between the variables h and r in the figure?
<IMAGE>
4. Applications of Derivatives
Related Rates
4:04 minutesProblem 3.95d
Textbook Question
Right circular cylinder The total surface area S of a right circular cylinder is related to the base radius r and height h by the equation S = 2πr² + 2πrh.
d. How is dr/dt related to dh/dt if S is constant?
Verified step by step guidance1
Start by understanding the problem: We have a right circular cylinder with a constant total surface area S, and we need to find the relationship between the rates of change of the radius (dr/dt) and the height (dh/dt).
Given the surface area formula S = 2πr² + 2πrh, differentiate both sides with respect to time t. Since S is constant, its derivative with respect to time is zero.
Apply the chain rule to differentiate the right side: dS/dt = 0 = d/dt(2πr²) + d/dt(2πrh).
Differentiate each term: The derivative of 2πr² with respect to t is 4πr(dr/dt), and the derivative of 2πrh with respect to t is 2πr(dh/dt) + 2πh(dr/dt).
Set up the equation from the derivatives: 0 = 4πr(dr/dt) + 2πr(dh/dt) + 2πh(dr/dt). Solve this equation for dr/dt in terms of dh/dt, r, and h.
Verified video answer for a similar problem:This video solution was recommended by our tutors as helpful for the problem above
Video duration:
4mWas this helpful?
Key Concepts
Here are the essential concepts you must grasp in order to answer the question correctly.
Implicit Differentiation
Implicit differentiation is a technique used to find the derivative of a function when it is not explicitly solved for one variable in terms of another. In this context, it allows us to differentiate the surface area equation with respect to time, treating both the radius and height as functions of time. This method is essential for relating the rates of change of the radius and height when the surface area is held constant.
Recommended video:
05:14
Finding The Implicit Derivative
Related Rates
Related rates involve finding the relationship between the rates of change of two or more variables that are related by an equation. In this problem, we are interested in how the rate of change of the radius (dr/dt) is connected to the rate of change of the height (dh/dt) while keeping the surface area constant. Understanding this concept is crucial for solving problems where multiple quantities change simultaneously.
Recommended video:
04:16Intro To Related Rates
Surface Area of a Cylinder
The surface area of a right circular cylinder is given by the formula S = 2πr² + 2πrh, which includes both the area of the circular bases and the lateral surface area. This formula is fundamental to the problem as it establishes the relationship between the radius, height, and surface area. Recognizing how changes in r and h affect S is key to determining the relationship between dr/dt and dh/dt when S is constant.
Recommended video:
09:07Example 1: Minimizing Surface Area
4:16mWatch next
Master Intro To Related Rates with a bite sized video explanation from Patrick
Start learningRelated Videos
Related Practice