Table of contents

0. Functions7h 52m
1. Limits and Continuity2h 2m
2. Intro to Derivatives1h 33m
3. Techniques of Differentiation3h 18m
4. Applications of Derivatives2h 38m
5. Graphical Applications of Derivatives6h 2m
6. Derivatives of Inverse, Exponential, & Logarithmic Functions2h 37m
7. Antiderivatives & Indefinite Integrals1h 26m
8. Definite Integrals4h 44m
9. Graphical Applications of Integrals2h 27m
- Area Between Curves
  1h 18m
- Introduction to Volume & Disk Method
  1h 8m
10. Physics Applications of Integrals 3h 16m
- Kinematics
  1h 13m
- Work
  2h 3m
11. Integrals of Inverse, Exponential, & Logarithmic Functions2h 34m
12. Techniques of Integration7h 39m
13. Intro to Differential Equations2h 55m
14. Sequences & Series5h 36m
15. Power Series2h 19m
- Introduction to Power Series
  1h 9m
- Taylor Series & Taylor Polynomials
  1h 10m
16. Parametric Equations & Polar Coordinates7h 58m

4. Applications of Derivatives

Related Rates

Calculus

4. Applications of Derivatives

Related Rates

Previous problemNext problem

2:35 minutes

Problem 3.95c

Textbook Question

Right circular cylinder The total surface area S of a right circular cylinder is related to the base radius r and height h by the equation S = 2πr² + 2πrh.

c. How is dS/dt related to dr/dt and dh/dt if neither r nor h is constant?

Verified step by step guidance

Start by identifying the given equation for the total surface area of the cylinder: \( S = 2\pi r^2 + 2\pi rh \).

Recognize that \( S \), \( r \), and \( h \) are all functions of time \( t \), so we need to use implicit differentiation with respect to \( t \).

Differentiate both sides of the equation with respect to \( t \). For the first term \( 2\pi r^2 \), use the chain rule: \( \frac{d}{dt}(2\pi r^2) = 4\pi r \frac{dr}{dt} \).

For the second term \( 2\pi rh \), apply the product rule: \( \frac{d}{dt}(2\pi rh) = 2\pi \left( r \frac{dh}{dt} + h \frac{dr}{dt} \right) \).

Combine the differentiated terms to express \( \frac{dS}{dt} \) in terms of \( \frac{dr}{dt} \) and \( \frac{dh}{dt} \): \( \frac{dS}{dt} = 4\pi r \frac{dr}{dt} + 2\pi \left( r \frac{dh}{dt} + h \frac{dr}{dt} \right) \).

Verified video answer for a similar problem:

This video solution was recommended by our tutors as helpful for the problem above

Video duration:

Play a video:

Was this helpful?

Key Concepts

Here are the essential concepts you must grasp in order to answer the question correctly.

Related Rates

Related rates involve finding the rate at which one quantity changes in relation to another. In this context, we are interested in how the surface area of a cylinder changes with respect to time as both the radius and height change. This concept is fundamental in calculus, as it allows us to connect different rates of change through derivatives.

Chain Rule

The chain rule is a fundamental principle in calculus used to differentiate composite functions. In the context of the given problem, it allows us to express the derivative of the surface area with respect to time as a function of the derivatives of the radius and height. This is crucial for relating the rates of change of different variables.

Surface Area of a Cylinder

The surface area of a right circular cylinder is given by the formula S = 2πr² + 2πrh, which includes contributions from both the circular bases and the lateral surface. Understanding this formula is essential for applying related rates, as it provides the relationship between the radius, height, and surface area that we need to differentiate with respect to time.

Watch next

Master Intro To Related Rates with a bite sized video explanation from Patrick

Start learning

Related Videos

Related Practice

Textbook Question

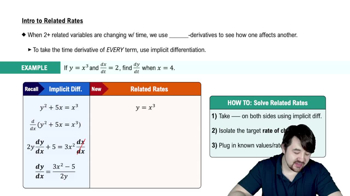
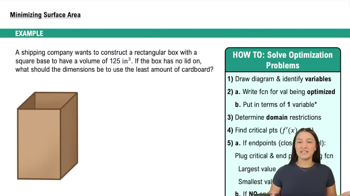
Resistors connected in parallel If two resistors of R₁ and R₂ ohms are connected in parallel in an electric circuit to make an R-ohm resistor, the value of R can be found from the equation

1/R = 1/R₁ + 1/R₂

<IMAGE>

If R₁ is decreasing at the rate of 1ohm/sec and R₂ is increasing at the rate of 0.5 ohm/sec, at what rate is R changing when R₁ = 75 ohms and R₂ = 50 ohms?

Textbook Question

Draining a tank Water drains from the conical tank shown in the accompanying figure at the rate of 5 ft³/min.

a. What is the relation between the variables h and r in the figure?

<IMAGE>

Textbook Question

Moving searchlight beam The figure shows a boat 1 km offshore, sweeping the shore with a searchlight. The light turns at a constant rate, dθ/dt = -0.6 rad/sec.

b. How many revolutions per minute is 0.6 rad/sec?

<IMAGE>

Textbook Question

Right circular cylinder The total surface area S of a right circular cylinder is related to the base radius r and height h by the equation S = 2πr² + 2πrh.

b. How is dS/dt related to dh/dt if r is constant?

Textbook Question

Right circular cylinder The total surface area S of a right circular cylinder is related to the base radius r and height h by the equation S = 2πr² + 2πrh.

d. How is dr/dt related to dh/dt if S is constant?

Textbook Question

Right circular cone The lateral surface area S of a right circular cone is related to the base radius r and height h by the equation

______

S = πr √ r² + h².

b. How is dS/dt related to dh/dt if r is constant?

Textbook Question

Economics

Marginal cost Suppose that the dollar cost of producing x washing machines is c(x) = 2000 + 100x − 0.1x².

a. Find the average cost per machine of producing the first 100 washing machines.

Textbook Question

Economics

Marginal cost Suppose that the dollar cost of producing x washing machines is c(x) = 2000 + 100x − 0.1x².

c. Show that the marginal cost when 100 washing machines are produced is approximately the cost of producing one more washing machine after the first 100 have been made, by calculating the latter cost directly.

Show more practices

Download the Mobile app

Privacy

Do not sell my personal information

Accessibility

Patent notice

Sitemap

Right circular cylinder The total surface area S of a right circular cylinder is related to the base radius r and height h by the equation S = 2πr² + 2πrh.c. How is dS/dt related to dr/dt and dh/dt if neither r nor h is constant?

Key Concepts

Related Rates

Chain Rule

Surface Area of a Cylinder

Watch next

Right circular cylinder The total surface area S of a right circular cylinder is related to the base radius r and height h by the equation S = 2πr² + 2πrh.

c. How is dS/dt related to dr/dt and dh/dt if neither r nor h is constant?