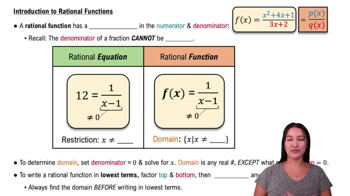
Theory and Examples
In Exercises 69 and 70, match each equation with its graph. Do not use a graphing device, and give reasons for your answer.
a. y = x⁴
b. y = x⁷
c. y = x¹⁰
<IMAGE>
 Verified step by step guidance
Verified step by step guidance Verified video answer for a similar problem:
Verified video answer for a similar problem: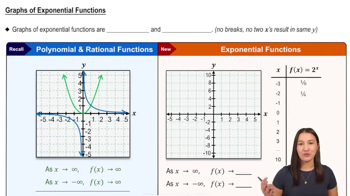


 5:57m
5:57mMaster Graphs of Common Functions with a bite sized video explanation from Patrick
Start learning