Explain why or why not Determine whether the following statements are true and give an explanation or counterexample.
b. d/dx(tan^−1 x) =sec² x
 Verified step by step guidance
Verified step by step guidance Verified video answer for a similar problem:
Verified video answer for a similar problem: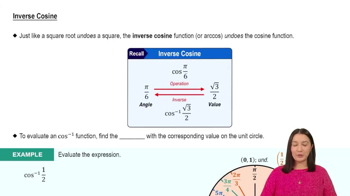



 7:26m
7:26mMaster Derivatives of Inverse Sine & Inverse Cosine with a bite sized video explanation from Patrick
Start learning