62–65. {Use of Tech} Graphing f and f'
c. Verify that the zeros of f' correspond to points at which f has a horizontal tangent line.
f(x)=(sec^−1 x)/x on [1,∞)
 Verified step by step guidance
Verified step by step guidance Verified video answer for a similar problem:
Verified video answer for a similar problem: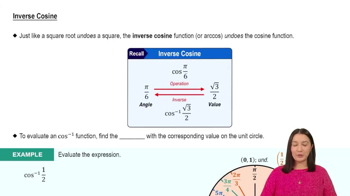

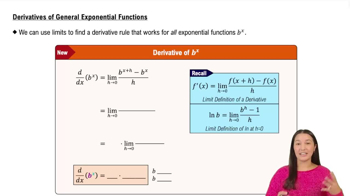

 7:26m
7:26mMaster Derivatives of Inverse Sine & Inverse Cosine with a bite sized video explanation from Patrick
Start learning