Identify the amplitude and period of the following functions.
Table of contents
- 0. Functions7h 54m
- Introduction to Functions16m
- Piecewise Functions10m
- Properties of Functions9m
- Common Functions1h 8m
- Transformations5m
- Combining Functions27m
- Exponent rules32m
- Exponential Functions28m
- Logarithmic Functions24m
- Properties of Logarithms36m
- Exponential & Logarithmic Equations35m
- Introduction to Trigonometric Functions38m
- Graphs of Trigonometric Functions44m
- Trigonometric Identities47m
- Inverse Trigonometric Functions48m
- 1. Limits and Continuity2h 2m
- 2. Intro to Derivatives1h 33m
- 3. Techniques of Differentiation3h 18m
- 4. Applications of Derivatives2h 38m
- 5. Graphical Applications of Derivatives6h 2m
- 6. Derivatives of Inverse, Exponential, & Logarithmic Functions2h 37m
- 7. Antiderivatives & Indefinite Integrals1h 26m
- 8. Definite Integrals4h 44m
- 9. Graphical Applications of Integrals2h 27m
- 10. Physics Applications of Integrals 3h 16m
- 11. Integrals of Inverse, Exponential, & Logarithmic Functions2h 31m
- 12. Techniques of Integration7h 41m
- 13. Intro to Differential Equations2h 55m
- 14. Sequences & Series5h 36m
- 15. Power Series2h 19m
- 16. Parametric Equations & Polar Coordinates7h 58m
0. Functions
Graphs of Trigonometric Functions
Problem 107
Textbook Question
Beginning with the graphs of y=sinx or y=cosx, use shifting and scaling transformations to sketch the graph of the following functions. Use a graphing utility to check your work.
q(x)=3.6cos(24πx)+2
 Verified step by step guidance
Verified step by step guidance1
Start with the basic graph of y = \cos(x), which is a cosine wave with an amplitude of 1, a period of 2\pi, and a midline at y = 0.
Apply a horizontal scaling transformation to the function. The term \frac{\pi x}{24} inside the cosine function indicates a horizontal stretch. The period of the cosine function is given by \frac{2\pi}{\frac{\pi}{24}} = 48. This means the graph completes one full cycle over an interval of 48 units on the x-axis.
Apply a vertical scaling transformation. The coefficient 3.6 in front of the cosine function indicates a vertical stretch. This changes the amplitude of the cosine wave from 1 to 3.6, meaning the wave will oscillate between -3.6 and 3.6.
Apply a vertical shift. The +2 at the end of the function indicates a vertical shift upwards by 2 units. This moves the midline of the cosine wave from y = 0 to y = 2, so the wave will now oscillate between -1.6 and 5.6.
Combine all transformations to sketch the graph of q(x) = 3.6\cos\left(\frac{\pi x}{24}\right) + 2. The graph is a cosine wave with a period of 48, an amplitude of 3.6, and a midline at y = 2. Use a graphing utility to verify the transformations and the final graph.
 Verified video answer for a similar problem:
Verified video answer for a similar problem:This video solution was recommended by our tutors as helpful for the problem above
Video duration:
7mPlay a video:
Was this helpful?
Key Concepts
Here are the essential concepts you must grasp in order to answer the question correctly.
Trigonometric Functions
Trigonometric functions, such as sine and cosine, are fundamental periodic functions that describe relationships between angles and sides in triangles. They are essential for modeling oscillatory behavior and are defined on the unit circle. Understanding their properties, such as amplitude, period, and phase shift, is crucial for graphing and transforming these functions.
Recommended video:

Introduction to Trigonometric Functions
Transformations of Functions
Transformations of functions involve shifting, stretching, compressing, or reflecting the graph of a function. For trigonometric functions, vertical shifts (adding or subtracting a constant) and horizontal shifts (changing the input variable) are common. These transformations allow us to manipulate the basic sine and cosine graphs to create new functions, such as the one given in the question.
Recommended video:
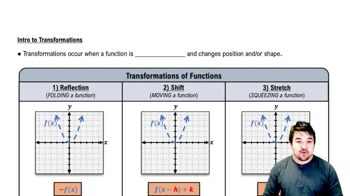
Intro to Transformations
Graphing Utilities
Graphing utilities are tools, often software or calculators, that allow users to visualize mathematical functions and their transformations. They can plot complex functions, helping to verify manual calculations and understand the behavior of functions over a range of values. Using a graphing utility is particularly useful for checking the accuracy of sketches and understanding the effects of transformations on the graph.
Recommended video:
Graphing The Derivative

 5:53m
5:53mWatch next
Master Graph of Sine and Cosine Function with a bite sized video explanation from Patrick
Start learningRelated Videos
Related Practice
Textbook Question
