Removable discontinuity Give an example of a function f (x) that is continuous for all values of x except x = 2, where it has a removable discontinuity. Explain how you know that f is discontinuous at x = 2, and how you know the discontinuity is removable.
Table of contents
- 0. Functions7h 54m
- Introduction to Functions16m
- Piecewise Functions10m
- Properties of Functions9m
- Common Functions1h 8m
- Transformations5m
- Combining Functions27m
- Exponent rules32m
- Exponential Functions28m
- Logarithmic Functions24m
- Properties of Logarithms36m
- Exponential & Logarithmic Equations35m
- Introduction to Trigonometric Functions38m
- Graphs of Trigonometric Functions44m
- Trigonometric Identities47m
- Inverse Trigonometric Functions48m
- 1. Limits and Continuity2h 2m
- 2. Intro to Derivatives1h 33m
- 3. Techniques of Differentiation3h 18m
- 4. Applications of Derivatives2h 38m
- 5. Graphical Applications of Derivatives6h 2m
- 6. Derivatives of Inverse, Exponential, & Logarithmic Functions2h 37m
- 7. Antiderivatives & Indefinite Integrals1h 26m
- 8. Definite Integrals4h 44m
- 9. Graphical Applications of Integrals2h 27m
- 10. Physics Applications of Integrals 3h 16m
- 11. Integrals of Inverse, Exponential, & Logarithmic Functions2h 31m
- 12. Techniques of Integration7h 41m
- 13. Intro to Differential Equations2h 55m
- 14. Sequences & Series5h 36m
- 15. Power Series2h 19m
- 16. Parametric Equations & Polar Coordinates7h 58m
1. Limits and Continuity
Continuity
Problem 2.5.69
Textbook Question
Use the Intermediate Value Theorem in Exercises 69–74 to prove that each equation has a solution. Then use a graphing calculator or computer grapher to solve the equations.
x³ − 3x − 1 = 0
 Verified step by step guidance
Verified step by step guidance1
Identify the function f(x) = x³ − 3x − 1 and note that it is a polynomial, which is continuous everywhere.
Choose an interval [a, b] where the function changes sign, indicating a root exists. For example, test f(0) and f(2).
Calculate f(0) = 0³ − 3(0) − 1 = -1 and f(2) = 2³ − 3(2) − 1 = 3. Since f(0) < 0 and f(2) > 0, there is a sign change.
Apply the Intermediate Value Theorem: Since f(x) is continuous on [0, 2] and f(0) < 0 < f(2), there exists at least one c in (0, 2) such that f(c) = 0.
Use a graphing calculator or computer grapher to approximate the root of the equation x³ − 3x − 1 = 0 within the interval [0, 2].
 Verified video answer for a similar problem:
Verified video answer for a similar problem:This video solution was recommended by our tutors as helpful for the problem above
Video duration:
4mPlay a video:
Was this helpful?
Key Concepts
Here are the essential concepts you must grasp in order to answer the question correctly.
Intermediate Value Theorem
The Intermediate Value Theorem states that if a continuous function f(x) takes on values f(a) and f(b) at two points a and b, and if f(a) and f(b) have opposite signs, then there exists at least one c in the interval (a, b) such that f(c) = 0. This theorem is crucial for proving the existence of a solution to the equation x³ − 3x − 1 = 0.
Recommended video:
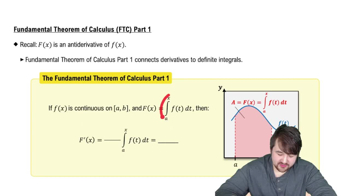
Fundamental Theorem of Calculus Part 1
Continuous Functions
A function is continuous if there are no breaks, jumps, or holes in its graph over its domain. For the Intermediate Value Theorem to apply, the function x³ − 3x − 1 must be continuous over the interval being considered. Polynomial functions, like this one, are continuous everywhere, which allows us to use the theorem effectively.
Recommended video:

Intro to Continuity
Graphical Analysis
Graphical analysis involves using a graphing calculator or computer software to visualize the function and identify where it crosses the x-axis, indicating a root. By graphing x³ − 3x − 1, we can visually confirm the existence of a solution and approximate its value, complementing the theoretical proof provided by the Intermediate Value Theorem.
Recommended video:
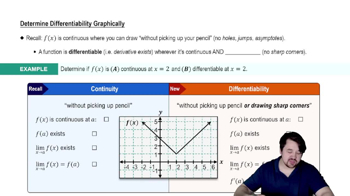
Determining Differentiability Graphically
Related Videos
Related Practice
Textbook Question


