Suppose the cost of producing x lawn mowers is C(x) = −0.02x²+400x+5000.
a. Determine the average and marginal costs for x = 3000 lawn mowers.
 Verified step by step guidance
Verified step by step guidance Verified video answer for a similar problem:
Verified video answer for a similar problem: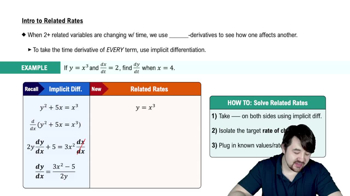



 4:16m
4:16mMaster Intro To Related Rates with a bite sized video explanation from Patrick
Start learning