In Exercises 39–42, express the given quantity in terms of sin x and cos x.
cos (3π/2 + x)
 Verified step by step guidance
Verified step by step guidance Verified video answer for a similar problem:
Verified video answer for a similar problem: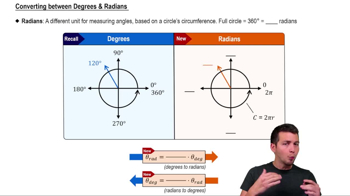


 6:36m
6:36mMaster Simplifying Trig Expressions with a bite sized video explanation from Patrick
Start learning