A rectangular swimming pool 10 ft wide by 20 ft long and of uniform depth is being filled with water.
c. At what rate is the water level rising if the pool is filled at a rate of 10ft³/min?
 Verified step by step guidance
Verified step by step guidance Verified video answer for a similar problem:
Verified video answer for a similar problem: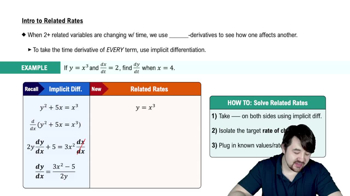


 4:16m
4:16mMaster Intro To Related Rates with a bite sized video explanation from Patrick
Start learning