At all times, the length of a rectangle is twice the width w of the rectangleas the area of the rectangle changes with respect to time t.
a. Find an equation relating A to w.
 Verified step by step guidance
Verified step by step guidance Verified video answer for a similar problem:
Verified video answer for a similar problem: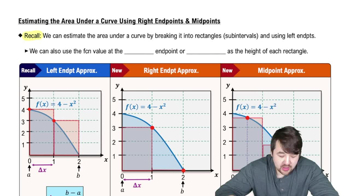
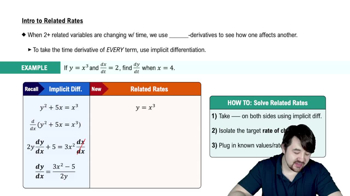


 4:16m
4:16mMaster Intro To Related Rates with a bite sized video explanation from Patrick
Start learning