Taxicab fees A taxicab ride costs \$3.50 plus \$2.50 per mile. Let m be the distance (in miles) from the airport to a hotel. Find and graph the function c(m) that represents the cost of taking a taxi from the airport to the hotel. Also determine how much it will cost if the hotel is 9 miles from the airport.
Table of contents
- 0. Functions7h 54m
- Introduction to Functions16m
- Piecewise Functions10m
- Properties of Functions9m
- Common Functions1h 8m
- Transformations5m
- Combining Functions27m
- Exponent rules32m
- Exponential Functions28m
- Logarithmic Functions24m
- Properties of Logarithms36m
- Exponential & Logarithmic Equations35m
- Introduction to Trigonometric Functions38m
- Graphs of Trigonometric Functions44m
- Trigonometric Identities47m
- Inverse Trigonometric Functions48m
- 1. Limits and Continuity2h 2m
- 2. Intro to Derivatives1h 33m
- 3. Techniques of Differentiation3h 18m
- 4. Applications of Derivatives2h 38m
- 5. Graphical Applications of Derivatives6h 2m
- 6. Derivatives of Inverse, Exponential, & Logarithmic Functions2h 37m
- 7. Antiderivatives & Indefinite Integrals1h 26m
- 8. Definite Integrals4h 44m
- 9. Graphical Applications of Integrals2h 27m
- 10. Physics Applications of Integrals 3h 16m
- 11. Integrals of Inverse, Exponential, & Logarithmic Functions2h 31m
- 12. Techniques of Integration7h 41m
- 13. Intro to Differential Equations2h 55m
- 14. Sequences & Series5h 36m
- 15. Power Series2h 19m
- 16. Parametric Equations & Polar Coordinates7h 58m
0. Functions
Common Functions
Problem 27
Textbook Question
Find the inverse function (on the given interval, if specified) and graph both f and f−1 on the same set of axes. Check your work by looking for the required symmetry in the graphs.
f(x)=8−4x
 Verified step by step guidance
Verified step by step guidance1
To find the inverse of the function \( f(x) = 8 - 4x \), start by replacing \( f(x) \) with \( y \), so we have \( y = 8 - 4x \).
Swap \( x \) and \( y \) to find the inverse function. This gives us \( x = 8 - 4y \).
Solve for \( y \) in terms of \( x \). Start by isolating \( y \) on one side: \( 4y = 8 - x \).
Divide both sides by 4 to solve for \( y \): \( y = \frac{8 - x}{4} \). This is the inverse function, \( f^{-1}(x) = \frac{8 - x}{4} \).
To graph both \( f(x) = 8 - 4x \) and \( f^{-1}(x) = \frac{8 - x}{4} \), plot them on the same set of axes. Check for symmetry about the line \( y = x \), which is a characteristic of inverse functions.
 Verified video answer for a similar problem:
Verified video answer for a similar problem:This video solution was recommended by our tutors as helpful for the problem above
Video duration:
12mPlay a video:
Was this helpful?
Key Concepts
Here are the essential concepts you must grasp in order to answer the question correctly.
Inverse Functions
An inverse function essentially reverses the effect of the original function. If a function f takes an input x and produces an output y, the inverse function f⁻¹ takes y as input and returns x. For a function to have an inverse, it must be one-to-one, meaning that each output is produced by exactly one input. This property ensures that the inverse function is well-defined.
Recommended video:
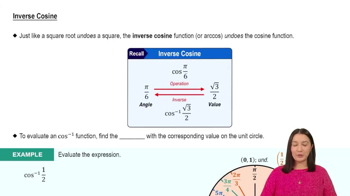
Inverse Cosine
Graphing Functions
Graphing functions involves plotting points on a coordinate system to visually represent the relationship between the input (x-values) and output (y-values). The graph of a function can reveal important characteristics such as intercepts, slopes, and asymptotic behavior. When graphing an inverse function, it is crucial to reflect the original function across the line y = x, which helps to illustrate the symmetry between a function and its inverse.
Recommended video:

Graph of Sine and Cosine Function
Symmetry in Graphs
Symmetry in graphs refers to the property where a graph remains unchanged under certain transformations. For functions and their inverses, this symmetry is observed about the line y = x. This means that if a point (a, b) lies on the graph of f, then the point (b, a) will lie on the graph of f⁻¹. Recognizing this symmetry is essential for verifying the correctness of the inverse function and understanding the relationship between the two graphs.
Recommended video:
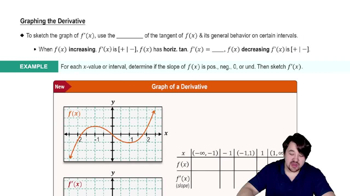
Graphing The Derivative

 5:57m
5:57mWatch next
Master Graphs of Common Functions with a bite sized video explanation from Patrick
Start learningRelated Videos
Related Practice
Textbook Question
