Here are the essential concepts you must grasp in order to answer the question correctly.
Infinite Limits
Infinite limits occur when the value of a function increases or decreases without bound as the input approaches a certain point. In this context, as x approaches 0, the function 4/x²/⁵ may tend towards infinity or negative infinity, depending on the behavior of the denominator, which becomes very small, causing the overall expression to grow very large.
Recommended video:
Behavior of Rational Functions
Rational functions are expressions involving ratios of polynomials. The behavior of these functions near points where the denominator approaches zero is crucial for determining limits. As x approaches 0 in 4/x²/⁵, the denominator x²/⁵ approaches zero, leading to a potential infinite limit, as the numerator remains constant and the denominator shrinks.
Recommended video:
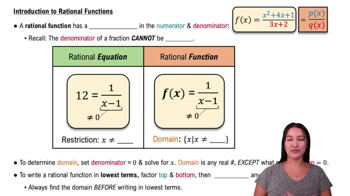
Intro to Rational Functions
Power Functions and Exponents
Understanding power functions and their exponents is essential for analyzing limits involving expressions like x²/⁵. The exponent determines how rapidly the function approaches zero or infinity as x approaches a specific value. In this case, x²/⁵ indicates a root, which affects the rate at which the denominator approaches zero, influencing the limit's behavior.
Recommended video:
 Verified step by step guidance
Verified step by step guidance Verified video answer for a similar problem:
Verified video answer for a similar problem:


 6:47m
6:47m