Here are the essential concepts you must grasp in order to answer the question correctly.
Surface Area of a Sphere
The surface area of a sphere is given by the formula A = 4πr², where r is the radius. This formula indicates that the surface area increases with the square of the radius. Understanding this relationship is crucial because the problem states that the rate of melting is proportional to this surface area, linking the geometry of the sphere to its rate of change.
Recommended video:
Example 1: Minimizing Surface Area
Rate of Change
In calculus, the rate of change refers to how a quantity changes in relation to another variable. In this context, we are interested in how the radius of the snowball changes over time as it melts. By establishing a relationship between the surface area and the radius, we can derive the rate of change of the radius with respect to time.
Recommended video:
Proportional Relationships
A proportional relationship means that one quantity changes at a constant rate relative to another. In this scenario, the rate at which the snowball melts is proportional to its surface area. This implies that as the surface area decreases, the radius will also change at a consistent rate, leading to the conclusion that the rate of change of the radius remains constant.
Recommended video:
Derivatives Applied To Velocity
 Verified step by step guidance
Verified step by step guidance Verified video answer for a similar problem:
Verified video answer for a similar problem: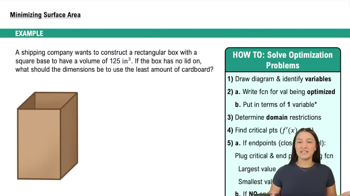

 4:16m
4:16m