The sides of a square decrease in length at a rate of 1 m/s.
b. At what rate are the lengths of the diagonals of the square changing?
 Verified step by step guidance
Verified step by step guidance Verified video answer for a similar problem:
Verified video answer for a similar problem: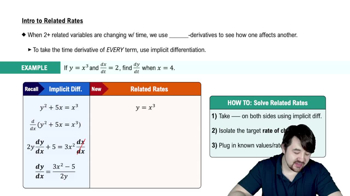


 4:16m
4:16mMaster Intro To Related Rates with a bite sized video explanation from Patrick
Start learning