Quadratic approximations
[Technology Exercise] e. Find the quadratic approximation to h(x) = √(1 + x) at x = 0. Graph h and its quadratic approximation together. Comment on what you see.
 Verified step by step guidance
Verified step by step guidance Verified video answer for a similar problem:
Verified video answer for a similar problem: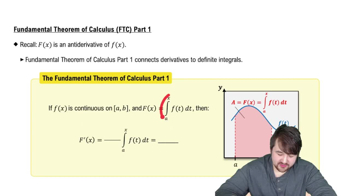


 5:53m
5:53mMaster Finding Differentials with a bite sized video explanation from Patrick
Start learning