Quadratic approximations
a. Let Q(x) = b₀ + b₁(x − a) + b₂(x − a)² be a quadratic approximation to f(x) at x = a with these properties:
i. Q(a) = f(a)
ii. Q′(a) = f′(a)
iii. Q″(a) = f″(a).
Determine the coefficients b₀, b₁, and b₂.
 Verified step by step guidance
Verified step by step guidance Verified video answer for a similar problem:
Verified video answer for a similar problem:
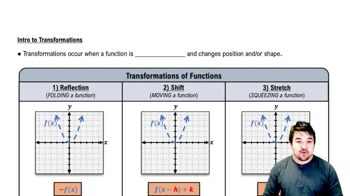
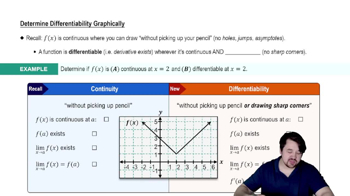

 5:53m
5:53mMaster Finding Differentials with a bite sized video explanation from Patrick
Start learning