Interpreting the derivative The graph of f' on the interval [-3,2] is shown in the figure. <IMAGE>


f. Sketch one possible graph of f.

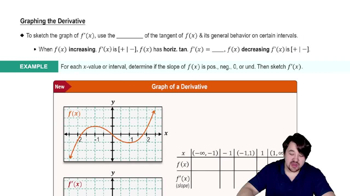
{Use of Tech} Fuel economy Suppose you own a fuel-efficient hybrid automobile with a monitor on the dashboard that displays the mileage and gas consumption. The number of miles you can drive with g gallons of gas remaining in the tank on a particular stretch of highway is given by m(g) = 50g−25.8g²+12.5g³−1.6g⁴, for 0≤g≤4.

b. Graph and interpret the gas mileage m(g)/g. 

Graphing functions Use the guidelines of this section to make a complete graph of f.

f(x) = x² - 6x

Designer functions Sketch the graph of a function f that is continuous on (-∞,∞) and satisfies the following sets of conditions.

f"(x) > 0 on (-∞,-2); f"(-2) = 0; f'(1) = 0; f"(2) = 0; f'(3) = 0; f"(x) > 0 on (4,∞)

Designer functions Sketch the graph of a function f that is continuous on (-∞,∞) and satisfies the following sets of conditions.

f'(x) > 0, for all x in the domain of f'; f'(-2) and f'(1) do not exist; f"(0) = 0

Sketch a graph of a function f with the following properties.

f' < 0 and f" < 0, for x < 3

Sketch a graph of a function f with the following properties.

f' < 0 and f" < 0, for x < -1

Sketch a continuous function f on some interval that has the properties described. Answers will vary.

The function f satisfies f'(-2) = 2, f'(0) = 0, f'(1) = -3 and f'(4) = 1.

Sketch a graph of a function f with the following properties.

f' < 0 and f" < 0, for 8 < x < 10