In Exercises 19–32, find the (a) domain and (b) range.
𝔂 = 3 cos x + 4 sin x (Hint: A trig identity is required.)
 Verified step by step guidance
Verified step by step guidance Verified video answer for a similar problem:
Verified video answer for a similar problem: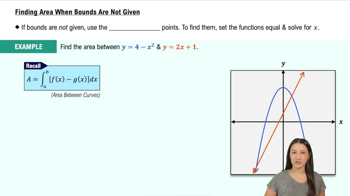


 1:36m
1:36mMaster Introduction to Calculus Channel with a bite sized video explanation from Patrick
Start learning