Consider the function f graphed here. The domain of f is the interval [−4, 6] and its graph is made of line segments joined end to end. " style="" width="350"> b. Graph the derivative of f. The graph should show a step function.

Consider the graph of G in the interval from -2 to 8. And we're given our graph here, which is a set of linear functions in piecewise. And we're given a graph to plot our derivative function. Now, to solve this, we did notice that every one of the functions on the piece wise is linear. So the derivative Of a linear function. It's just the slope of each line segment. So what we're going to do is find the slope of every one of the piece-wise line segments on our function. Let's say we look at. -20. 20-3 1st. Our slope Or B the change in Y divided by the change in X or -3 minus 0 divided by 0 minus -2. This gives us -3 divided by 2 or 1.5. We will repeat this for every segment. Our next one goes from 0-3. 236. Which will be 6 minus -3. Divided by 3 minus 0. Which is 9 divided by 3 or 3. We then had the segment from 36 to 56. Which will be 6 minus 6. Divided by 5 minus 3, which is just 0. And finally We have the segment in 5628-3. Which will be -3, minus 6 divided by 8, minus 5. Or -9 divided by 3, which is -3. We now have 4 different slopes for 4 different line segments. Now, notice that our derivative is not going to be continuous. In particular, will have discontinuities at every end of the line segment. So, I will note, we have This kind of news At -2035 and 8. So now, when we go to sketch the graph of our derivative. We have our first one From 20. And 03 being -1.5. So From -2 to 0, we go down to -1.5. And because we have this continuity. We have an open circle. We will draw a straight line between them, that's horizontal. Our next one goes from 0 to 3. And that derivative is 3. So, from 0, we go up to 3, and end at 3. We then have our slope being 0. From the 036 to 56. So from 3 to 5. Our value is 0. And finally From 5 to 8, our slope is -3. So We go down to -3 and draw a line segment. Between those two points. This would give the answer. Or our derivatives graph. OK, I hope to help you solve the problem. Thank you for watching. Goodbye.

Table of contents

Skip topic navigation

0. Functions7h 52m
1. Limits and Continuity2h 2m
2. Intro to Derivatives1h 33m
3. Techniques of Differentiation3h 18m
4. Applications of Derivatives2h 38m
5. Graphical Applications of Derivatives6h 2m
6. Derivatives of Inverse, Exponential, & Logarithmic Functions2h 37m
7. Antiderivatives & Indefinite Integrals1h 26m
8. Definite Integrals4h 44m
9. Graphical Applications of Integrals2h 27m
- Area Between Curves
  1h 18m
- Introduction to Volume & Disk Method
  1h 8m
10. Physics Applications of Integrals 3h 16m
- Kinematics
  1h 13m
- Work
  2h 3m
11. Integrals of Inverse, Exponential, & Logarithmic Functions2h 34m
12. Techniques of Integration7h 39m
13. Intro to Differential Equations2h 55m
14. Sequences & Series5h 36m
15. Power Series2h 19m
- Introduction to Power Series
  1h 9m
- Taylor Series & Taylor Polynomials
  1h 10m
16. Parametric Equations & Polar Coordinates7h 58m

2. Intro to Derivatives

Derivatives as Functions

Calculus

2. Intro to Derivatives

Derivatives as Functions

Previous problemNext problem

4:33 minutes

Problem 3.2.31b

Textbook Question

Consider the function f graphed here. The domain of f is the interval [−4, 6] and its graph is made of line segments joined end to end.

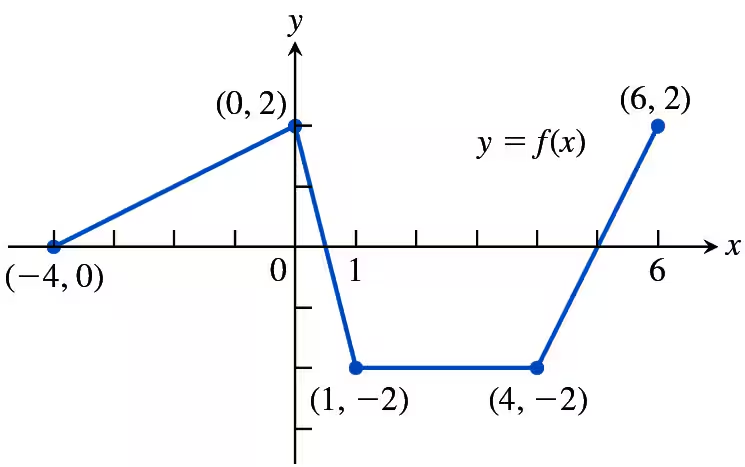
b. Graph the derivative of f. The graph should show a step function.

Verified step by step guidance

Step 1: Analyze the graph of f(x). The function is piecewise linear, composed of line segments joined end to end. The domain is [−4, 6], and the graph has vertices at (−4, 0), (0, 2), (1, −2), (4, −2), and (6, 2).

Step 2: Recall that the derivative of a function represents the slope of the tangent line at any given point. For a piecewise linear function, the derivative is constant within each segment since the slope does not change.

Step 3: Calculate the slope of each segment: - From (−4, 0) to (0, 2), the slope is \( \frac{2 - 0}{0 - (-4)} = \frac{2}{4} = \frac{1}{2} \). - From (0, 2) to (1, −2), the slope is \( \frac{-2 - 2}{1 - 0} = \frac{-4}{1} = -4 \). - From (1, −2) to (4, −2), the slope is \( \frac{-2 - (-2)}{4 - 1} = \frac{0}{3} = 0 \). - From (4, −2) to (6, 2), the slope is \( \frac{2 - (-2)}{6 - 4} = \frac{4}{2} = 2 \).

Step 4: Represent the derivative as a step function. The derivative is constant within each interval: - On [−4, 0], the derivative is \( \frac{1}{2} \). - On [0, 1], the derivative is −4. - On [1, 4], the derivative is 0. - On [4, 6], the derivative is 2.

Step 5: Sketch the graph of the derivative. The graph will be a step function with constant values: - A horizontal line at \( \frac{1}{2} \) from x = −4 to x = 0. - A horizontal line at −4 from x = 0 to x = 1. - A horizontal line at 0 from x = 1 to x = 4. - A horizontal line at 2 from x = 4 to x = 6.

Verified video answer for a similar problem:

This video solution was recommended by our tutors as helpful for the problem above

Video duration:

Play a video:

Was this helpful?

Key Concepts

Here are the essential concepts you must grasp in order to answer the question correctly.

Derivative of a Function

The derivative of a function at a point measures the rate at which the function value changes as its input changes. For a piecewise linear function, the derivative is constant on each segment, representing the slope of the line. In this graph, the derivative will be a step function, indicating constant slopes between the given points.

Piecewise Linear Functions

A piecewise linear function is composed of straight line segments. Each segment has a constant slope, which is the derivative of the function over that interval. Understanding the slopes of these segments is crucial for graphing the derivative, as each segment's slope corresponds to a constant value in the derivative's graph.

Step Functions

A step function is a piecewise function that jumps from one constant value to another at specific points. When graphing the derivative of a piecewise linear function, the result is a step function, where each step corresponds to the slope of a segment in the original function. This graph will have horizontal lines at the slope values, changing at the endpoints of each segment.

Watch next

Master Derivatives with a bite sized video explanation from Patrick

Start learning