Owlet talons Let L (t) equal the average length (in mm) of the middle talon on an Indian spotted owlet that is t weeks old, as shown in the figure.<IMAGE>
a. Estimate L' (1.5) and state the physical meaning of this quantity.
 Verified step by step guidance
Verified step by step guidance Verified video answer for a similar problem:
Verified video answer for a similar problem: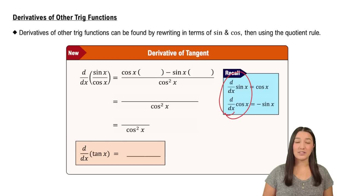



 6:15m
6:15mMaster Graphing The Derivative with a bite sized video explanation from Patrick
Start learning