Textbook Question
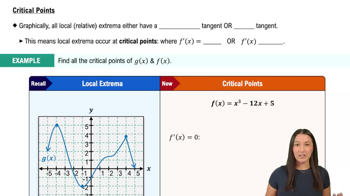
Locating extrema Consider the graph of a function ƒ on the interval [-3, 3]. <IMAGE>
d. Give the approximate coordinates of the zero(s) of f.
5. Graphical Applications of Derivatives
Intro to Extrema
6:07 minutesProblem 4.3.38
Textbook Question
Increasing and decreasing functions. Find the intervals on which f is increasing and the intervals on which it is decreasing.
f(x) = x ln x - 2x + 3 on (0,∞)
Verified step by step guidance1
First, find the derivative of the function f(x) = x ln x - 2x + 3. Use the product rule for the term x ln x, which states that if u(x) = x and v(x) = ln x, then the derivative is u'(x)v(x) + u(x)v'(x).
Calculate the derivative: f'(x) = (1)(ln x) + (x)(1/x) - 2. Simplify this to get f'(x) = ln x + 1 - 2.
Simplify the expression for the derivative: f'(x) = ln x - 1.
Determine the critical points by setting the derivative equal to zero: ln x - 1 = 0. Solve for x to find the critical points.
Analyze the sign of f'(x) on the intervals determined by the critical points. If f'(x) > 0, the function is increasing on that interval; if f'(x) < 0, the function is decreasing. Use test points in each interval to determine the sign of f'(x).
Verified video answer for a similar problem:This video solution was recommended by our tutors as helpful for the problem above
Video duration:
6mWas this helpful?
Key Concepts
Here are the essential concepts you must grasp in order to answer the question correctly.
Derivative
The derivative of a function measures the rate at which the function's value changes as its input changes. It is a fundamental tool in calculus for determining the slope of the tangent line to the curve at any point. For a function to be increasing, its derivative must be positive, while a negative derivative indicates that the function is decreasing.
Recommended video:
05:44
Derivatives
Critical Points
Critical points occur where the derivative of a function is zero or undefined. These points are essential for analyzing the behavior of the function, as they can indicate potential local maxima, minima, or points of inflection. To determine intervals of increase or decrease, one must find these critical points and test the sign of the derivative in the intervals they create.
Recommended video:
04:50Critical Points
First Derivative Test
The First Derivative Test is a method used to determine whether a function is increasing or decreasing on specific intervals. By evaluating the sign of the derivative before and after each critical point, one can conclude whether the function transitions from increasing to decreasing or vice versa. This test provides a systematic approach to understanding the function's overall behavior.
Recommended video:
07:09The First Derivative Test: Finding Local Extrema
5:58mWatch next
Master Finding Extrema Graphically with a bite sized video explanation from Patrick
Start learningRelated Videos
Related Practice