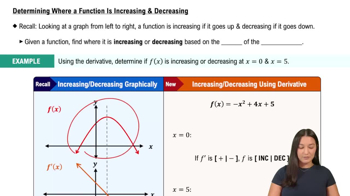
Locating extrema Consider the graph of a function ƒ on the interval [-3, 3]. <IMAGE>
a . Give the approximate coordinates of the local maxima and minima of ƒ
 Verified step by step guidance
Verified step by step guidance Verified video answer for a similar problem:
Verified video answer for a similar problem:


 5:58m
5:58mMaster Finding Extrema Graphically with a bite sized video explanation from Patrick
Start learning