Use three rectangles to approximate the area under the curve of f ( x ) = 3 ( x − 2 ) 2 f\left(x\right)=3\left(x-2\right)^2 from x = 0 x=0 to x = 3 x=3 using the midpoint rule.

in this problem, we're asked to use three rectangles to approximate the area under the curve of this function, f of x equals three times x minus two squared, and that's going to be from x equals zero to x equals three using the midpoint rule. So let's go ahead and see how we can solve this. Now our goal with any of these types of problems where we're estimating the area under these curves, is to fill the curve with rectangles to get the approximate area. And to do this, each rectangle is going to have a certain width and height, which we need to find the area of all of them, to go ahead and figure out what that area is approximately under the curve. And the width of each rectangle is gonna be delta x. Delta x can be calculated with this equation, b minus a over n, the number of rectangles. Now b is gonna be the end of our interval, which is three minuteus a, which is the start of our interval, zero, all divided by the number of rectangles which we have, which in this case is three. So we have three minuteus zero over three, which is one. So that's going to be the width of each rectangle. Now, what we're doing is filling this curve with rectangles from zero to three, all with the width of one. Now, we're using the midpoint rule, so what we need to do is go to the midpoints of each of these rectangles. Now, our first rectangle will have a width of one, it's going to start at zero, so we're going to have this width right here. And going to the midpoint, that's 0.5, so it's going to touch the curve right about there. So this is going to be our first rectangle that we can draw underneath this curve. Now next, we'll go to this point right here, which is between one and two. So we can go over another width, and then we can check this middle point at 1.5, and that's going to give us this next rectangle right here. Then lastly, we we can go to a point between two and the end of this interval, which is three. So I'm gonna extend this a little bit to give us a three here, and so we're going to go to this point right about here. So going to this point, we're gonna touch the curve there, and then that's going to be our next rectangle that we look at. So this here is going to be the heights of each of our rectangles as well as the widths, and so what we need to do is find the heights, so that way we can calculate the area of each one, thus for estimating the area under the curve of this function. Now the way that I can do this is by adding up the area of each rectangle, area one plus area two plus area three. And I know that each rectangle is going to have an area of width times height. Now the width of each of these rectangles we already figured out is delta x. So I'm gonna pull delta x out front of this equation here, and then we're going to multiply this by the heights of each rectangle. Now the heights of each one are going to depend on the midpoints into our function. So we'll take this x value, the midpoint, and plug it into our function, which is this function up here. So we're first gonna have f of 0.5. We're going to have plus this midpoint right here, which is f of 1.5, plus this midpoint plugged into our function here, which is f of 2.5. Just taking those midpoints, plugging them into our function. Now from here, we're going to deal with the numbers. So we have this delta x, which we already calculated to be one, and that's going to be multiplied by f of 0.5. If you take 0.5 and you plug it into this function up here, you'd have 0.5 minus two squared times three. That's all going to come out to 6.75. Then what you need to do is take 1.5 and plug it into this function, and if you do that, you'll get 0.75. Then what you need to do is take 2.5 and plug it into this function, and that's going to give you 0.75 again. So these are gonna be the results if you plug these into your function, and this is what all the numbers come out to. So what you can do is add everything in these brackets here, multiply it by one, and you should get a result of 8.25 as the approximate area under the curve of this function. So this right here is the estimation, and the solution to this problem using the midpoint rule. So hope you found this video helpful, and let's move on and get some more practice.

8. Definite Integrals

Estimating Area with Finite Sums

Calculus

8. Definite Integrals

Estimating Area with Finite Sums

Struggling with Calculus?

Join thousands of students who trust us to help them ace their exams!Watch the first video

Multiple Choice

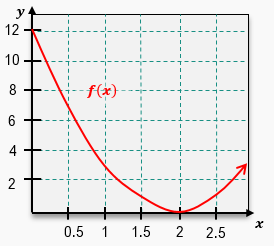
Use three rectangles to approximate the area under the curve of $f (x) = 3 {(x - 2)}^{2}$ from $x equals 0$ to $x equals 3$ using the midpoint rule.

$A equals 9.00$

$A equals 6.00$

$A equals 8.25$

$A equals 15.0$

Verified step by step guidance

Identify the function f(x) = 3(x - 2)^2 and the interval [0, 3] over which we need to approximate the area under the curve using the midpoint rule.

Divide the interval [0, 3] into 3 equal subintervals. Each subinterval will have a width of Δx = (3 - 0) / 3 = 1.

Determine the midpoints of each subinterval. For the subintervals [0, 1], [1, 2], and [2, 3], the midpoints are x = 0.5, x = 1.5, and x = 2.5, respectively.

Evaluate the function f(x) at each midpoint: f(0.5), f(1.5), and f(2.5). This will give the heights of the rectangles.

Calculate the area of each rectangle using the formula Area = f(midpoint) * Δx, and sum these areas to approximate the total area under the curve.

7:59m

Watch next

Master Estimating the Area Under a Curve Using Left Endpoints with a bite sized video explanation from Patrick

Start learning

Estimating Area with Finite Sums practice set

Problem sets built by lead tutors

Expert video explanations

Go to Practice

Struggling with Calculus?

Use three rectangles to approximate the area under the curve of f(x)=3(x−2)2f\left(x\right)=3\left(x-2\right)^2 from x=0x=0 to x=3x=3 using the midpoint rule.

Watch next

Estimating Area with Finite Sums practice set

Use three rectangles to approximate the area under the curve of $f (x) = 3 {(x - 2)}^{2}$ from $x equals 0$ to $x equals 3$ using the midpoint rule.