Use shifts and scalings to graph the given functions. Then check your work with a graphing utility. Be sure to identify an original function on which the shifts and scalings are performed.
 Verified step by step guidance
Verified step by step guidance Verified video answer for a similar problem:
Verified video answer for a similar problem: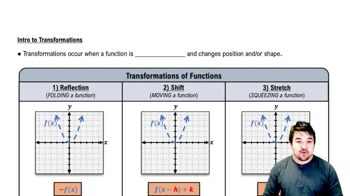



 5:25m
5:25mMaster Intro to Transformations with a bite sized video explanation from Patrick
Start learning