Graph the given function. g ( x ) = e x + 3 − 1 g\left(x\right)=e^{x+3}-1 g ( x ) = e x + 3 − 1

In this problem, we're asked to graph the given function. And here the function we have is g of x is equal to e to the power of x plus 3 minuteus 1. Now we just learned that we can treat the number e just like we would any other number, so we can also graph this exponential function just like we would any other exponential function using transformations. So let's go ahead and get started with step 0 and identify and graph our parent function. Now here in my function, I can see this e to the power of x, which represents my parent function, and I've just undergone these transformations here. So my parent function is f of x is equal to e to the power of x. And we can plot this just like we would any other exponential function. So we're going to plot this at negative one one over b, which in this case, b is e, which we know is equal to about 2.718. Now you might just want to put in your calculator 1 over e to get this value, and you'll get about 0.37. Then 1, that point still stays the same. And then 1 b, so in this case, 1 e. Now, again, we know that e is about 2.718 and so on, So I can just graph this at about 2.7 on my graph. So let's go ahead and plot these points. So negative one, getting close to that x axis there, 1, same point as always, and then 1 about 2.7 somewhere up here. So I can go ahead and connect this. And I know that I still have my horizontal asymptote at y equals 0, which I can plot as well using a dash line, just like any other exponential function. Now we can go ahead and start graphing our new function with transformations. Now we're first going to shift our horizontal asymptote to y equals k. Now looking at my function here, I see that it's x plus 3 minus 1. And now this negative one represents my vertical shift. So this is my value for k, negative one. So I'm gonna go ahead and plot that horizontal asymptote at y equals negative one using a dash line. Now moving on to step 2, we want to see if there's a reflection happening. Now looking at my function here, I don't have any negatives that got inserted outside or inside of my function, so I don't have to worry about a reflection here. And I can go ahead and move on to the second part of step 2, which is to shift my test points by h k. Now looking at my function, I have this x plus 3 in the exponent here, which means that my value for h is negative 3 because, remember, we consider x minus h, so this would be the same thing as x minus negative 3. So my value for h is negative 3, which represents my horizontal shift. Then we already identified k as negative one so let's go ahead and take the points from our original function and shift them by those values. So we're gonna go ahead and shift this first point. We're gonna go 3 over to the left and then one value down, so we're gonna end up right down here. Now for my next point, I'm going to do the same thing. Go 1, 2, 3 over and then one down ending up right here. And then my final point to 1, 2, 3 over and then a one down, I'm going to end up right about here. Now, I have my new points and I can go ahead and connect them using a smooth curve and approaching that asymptote. So let's go ahead and connect our new points here. That's going to curve upward and then approach the asymptote towards the bottom there. So this is our new curve. Let's go ahead and identify that domain and range. Now remember, our domain is always, always going to be all real numbers. That doesn't change when we have a value of e in our exponential function. And then for our range, we need to look at whether our function is above or below our asymptote. And since my asymptote is here, my function is above it. So that means that my range is going to go from k to infinity which in this case k is negative one so my range is from negative one to infinity. Now Now that we've been able to graph this exponential function let's keep going.

Table of contents

Skip topic navigation

0. Fundamental Concepts of Algebra3h 32m
1. Equations and Inequalities3h 27m
2. Graphs1h 43m
3. Functions & Graphs2h 17m
4. Polynomial Functions1h 54m
5. Rational Functions1h 23m
6. Exponential and Logarithmic Functions2h 28m
7. Measuring Angles40m
8. Trigonometric Functions on Right Triangles2h 5m
9. Unit Circle1h 19m
10. Graphing Trigonometric Functions1h 19m
11. Inverse Trigonometric Functions and Basic Trig Equations1h 41m
12. Trigonometric Identities 2h 34m
13. Non-Right Triangles1h 38m
14. Vectors2h 25m
15. Polar Equations2h 5m
16. Parametric Equations1h 6m
17. Graphing Complex Numbers1h 7m
18. Systems of Equations and Matrices3h 6m
19. Conic Sections2h 36m
20. Sequences, Series & Induction1h 15m
21. Combinatorics and Probability1h 45m
22. Limits & Continuity1h 49m
23. Intro to Derivatives & Area Under the Curve2h 9m

6. Exponential and Logarithmic Functions

The Number e

Precalculus

6. Exponential and Logarithmic Functions

The Number e

Previous problemNext problem

Struggling with Precalculus?

Join thousands of students who trust us to help them ace their exams!Watch the first video

Multiple Choice

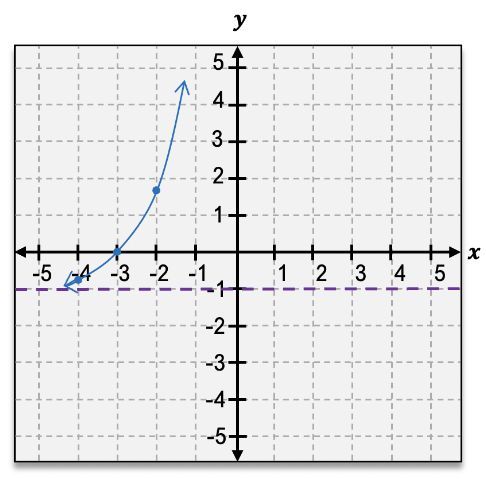
Graph the given function.
$g\left(x\right)=e^{x+3}-1$

Previous problemNext problem

Verified step by step guidance

Identify the base function: The given function is g(x) = e^(x+3) - 1. The base function is f(x) = e^x, which is an exponential function with a horizontal asymptote at y = 0.

Determine the transformations: The function g(x) = e^(x+3) - 1 involves two transformations of the base function f(x) = e^x. The '+3' inside the exponent indicates a horizontal shift to the left by 3 units, and the '-1' outside the exponent indicates a vertical shift downward by 1 unit.

Identify the new horizontal asymptote: The vertical shift of -1 unit moves the horizontal asymptote from y = 0 to y = -1.

Plot key points: Start by plotting the point that corresponds to the y-intercept of the base function, which is (0, 1) for f(x) = e^x. Apply the transformations to this point: shift left by 3 units to (-3, 1) and then down by 1 unit to (-3, 0).

Sketch the graph: Draw the curve starting from the transformed y-intercept, approaching the horizontal asymptote y = -1 as x approaches negative infinity, and rising steeply as x increases, reflecting the exponential growth of the function.