The ideal gas law, represented by the equation \( PV = nRT \), describes the relationship between pressure (P), volume (V), number of moles (n), the gas constant (R), and temperature (T). Understanding how these variables interact is crucial for solving problems related to gases.
When examining the relationship between pressure and volume, we can rearrange the ideal gas law to isolate these variables. By setting \( nRT \) as a constant, we can express pressure as inversely proportional to volume: \( P = \frac{k}{V} \), where \( k \) is a constant. This indicates that as volume increases, pressure decreases, and vice versa. Thus, pressure and volume exhibit an inverse relationship.
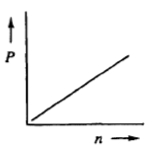
Next, we explore the relationship between pressure and the number of moles. Keeping volume, R, and T constant, we find that pressure is directly proportional to the number of moles: \( P \propto n \). This means that increasing the number of moles will result in an increase in pressure, as both variables rise together.
Similarly, when considering pressure and temperature, we again find a direct relationship: \( P \propto T \). This indicates that an increase in temperature will lead to an increase in pressure, assuming the other variables remain constant.
Now, let’s analyze the relationship between volume and moles. By isolating these variables while ignoring pressure, R, and T, we see that volume is directly proportional to the number of moles: \( V \propto n \). Thus, increasing the volume will also increase the number of moles present in the gas.
Finally, we look at the relationship between volume and temperature. Similar to the previous relationships, volume and temperature are directly proportional: \( V \propto T \). An increase in temperature will result in an increase in volume, provided the other variables are held constant.
In summary, the ideal gas law reveals that pressure and volume are inversely related, while pressure and moles, pressure and temperature, volume and moles, and volume and temperature are all directly proportional. Understanding these relationships is essential for predicting how changes in one variable will affect others in gas-related scenarios.