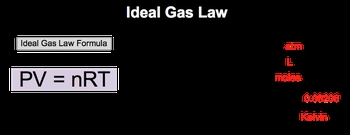
The Ideal Gas Law: Videos & Practice Problems

In the study of gas behavior, the ideal gas law serves as a fundamental equation that describes how gases respond to changes in pressure, volume, moles, and temperature. The ideal gas law is expressed by the formula:

\( PV = nRT \)

In this equation, \( P \) represents pressure, measured in atmospheres (atm), \( V \) denotes volume in liters (L), \( n \) indicates the number of moles of gas, \( R \) is the ideal gas constant, and \( T \) signifies temperature in Kelvins (K). The value of the gas constant \( R \) commonly used in this context is \( 0.08206 \, \text{L} \cdot \text{atm} / (\text{mol} \cdot \text{K}) \).

Understanding the ideal gas law is crucial, as it is frequently applied in various calculations and concepts throughout the study of gases. Mastery of this formula will be essential for solving problems related to gas behavior under different conditions.

The ideal gas law, represented by the equation PV = nRT, is a fundamental equation in chemistry that relates pressure (P), volume (V), number of moles (n), the ideal gas constant (R), and temperature (T). To effectively use this equation, it is crucial to ensure that all variables are expressed in the correct units.

First, pressure must be converted to atmospheres. In this case, we start with a pressure of 600 millimeters of mercury (mmHg). The conversion factor is that 1 atmosphere is equivalent to 760 mmHg. Therefore, the conversion is performed as follows:

P = \frac{600 \text{ mmHg}}{760 \text{ mmHg/atm}} \approx 0.789 \text{ atm}

Next, the volume must be in liters. Given a volume of 500 milliliters, we convert this to liters by recognizing that 1 milliliter equals 0.001 liters:

V = 500 \text{ mL} \times 0.001 \text{ L/mL} = 0.500 \text{ L}

For the number of moles, we need to convert the mass of nitrogen gas (N₂) into moles. The molar mass of nitrogen gas is calculated as follows: each nitrogen atom has a mass of 14.01 grams, and since nitrogen gas is diatomic (N₂), the molar mass is:

M = 2 \times 14.01 \text{ g} = 28.02 \text{ g/mol}

Thus, to find the number of moles from 29.3 grams of N₂, we use the formula:

n = \frac{29.3 \text{ g}}{28.02 \text{ g/mol}} \approx 1.05 \text{ moles}

Finally, temperature must be expressed in Kelvin. To convert from Celsius to Kelvin, we add 273.15 to the Celsius temperature. For a temperature of 50 degrees Celsius, the conversion is:

T = 50 + 273.15 = 323.15 \text{ K}

In summary, for the ideal gas law, the necessary units are:

• Pressure (P) in atmospheres: 0.789 atm
• Volume (V) in liters: 0.500 L
• Number of moles (n): 1.05 moles
• Temperature (T) in Kelvin: 323.15 K

Understanding these conversions and the correct units is essential for accurately applying the ideal gas law in various chemical calculations.

The ideal gas law is a fundamental equation in chemistry that relates the pressure, volume, temperature, and number of moles of a gas. A key component of this law is the gas constant, denoted as R, which can take on two different values depending on the context of the problem. The first value, R = 0.08206 L·atm/(mol·K), is commonly used when applying the ideal gas law. This value is particularly useful in calculations involving gases under standard conditions.

In contrast, the second value of the gas constant, R = 8.314 J/(mol·K), is utilized in scenarios involving energy, speed, or velocity. This is particularly relevant when dealing with the kinetic energy of particles or the energy changes in chemical reactions. Understanding when to use each value is crucial for accurate calculations.

To convert between these two forms of the gas constant, it is important to recognize the relationship between liters times atmospheres and joules. Specifically, the conversion factor states that 1 L·atm = 101.325 J. By using this conversion factor, one can effectively switch between the two values of R. For instance, when converting 0.08206 L·atm/(mol·K) to joules, the liters times atmospheres cancel out, leading to the simplified value of 8.314 J/(mol·K) for practical use in energy-related calculations.

In summary, the gas constant R is essential for various calculations in chemistry, and recognizing its two distinct values allows for accurate application in different contexts, whether dealing with the ideal gas law or energy dynamics.

To determine the number of moles of ammonia in a 25-liter tank at 190 degrees Celsius and 5.20 atmospheres, we can utilize the ideal gas law, represented by the equation:

PV = nRT

In this equation, P stands for pressure, V is volume, n represents the number of moles, R is the ideal gas constant, and T is temperature in Kelvin. Our goal is to isolate the variable for moles (n), which can be expressed as:

n = \frac{PV}{RT}

Given the values:

• P = 5.20 atm
• V = 25 L
• R = 0.08206 L·atm/(mol·K)
• T = 190 °C

First, we need to convert the temperature from Celsius to Kelvin:

T = 190 + 273.15 = 463.15 K

Now, substituting the values into the equation:

n = \frac{(5.20 \, \text{atm}) \times (25 \, \text{L})}{(0.08206 \, \text{L·atm/(mol·K)}) \times (463.15 \, \text{K})}

Calculating the numerator:

5.20 \times 25 = 130 \, \text{atm·L}

Calculating the denominator:

0.08206 \times 463.15 \approx 38.036 \, \text{L·atm/(mol·K)}

Now, dividing the two results:

n \approx \frac{130}{38.036} \approx 3.4205 \, \text{moles}

When considering significant figures, the least number of significant figures in the given data is 2 (from 5.20). Therefore, we round our final answer to:

n = 3.4 \, \text{moles of ammonia}

This process illustrates the application of the ideal gas law to find the number of moles, emphasizing the importance of unit consistency and significant figures in calculations.