Density of Geometric Objects: Videos & Practice Problems

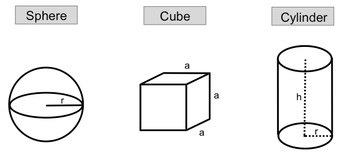
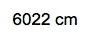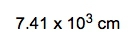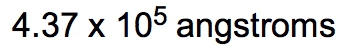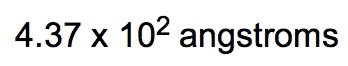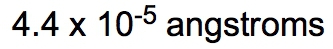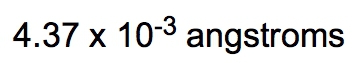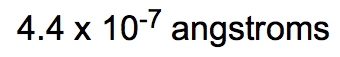Density is defined as the mass of an object divided by its volume, expressed mathematically as:

D = \frac{m}{V}

where D is density, m is mass, and V is volume. This concept can be applied to various geometric objects, each with its own volume formula.

For a sphere, the volume can be calculated using the formula:

V = \frac{4}{3} \pi r^3

Here, r represents the radius, which is the distance from the center of the sphere to its surface. Understanding this formula allows you to determine the volume of a sphere when the radius is known.

In the case of a cube, where all sides are equal in length, the volume is given by:

V = a^3

In this formula, a denotes the length of one edge of the cube. This straightforward relationship makes it easy to calculate the volume of a cube based on the length of its sides.

For a cylinder, the volume is determined by both the radius and the height, expressed as:

V = \pi r^2 h

In this equation, r is the radius of the base of the cylinder, and h is the height. This formula highlights the importance of both dimensions in calculating the volume of a cylinder.

Once the volume of these geometric shapes is established, you can relate it back to density by rearranging the density formula to find mass or volume as needed. This foundational understanding of density and volume is crucial for solving various physics and engineering problems involving geometric objects.

To determine the mass of a cube of silver measuring 0.56 meters on each side, we start by recognizing the density of silver, which is 10.5 grams per cubic centimeter (g/cm³). The first step is to calculate the volume of the cube using the formula for volume:

Volume = length³

Given that each side of the cube is 0.56 meters, we convert this measurement to centimeters (1 meter = 100 centimeters), resulting in:

0.56 m = 56 cm

Now, we can calculate the volume:

Volume = (56 cm)³ = 175616 cm³

Next, we apply the density to find the mass. Density is defined as mass per unit volume, which can be rearranged to find mass:

Mass = Density × Volume

Substituting the known values:

Mass = 10.5 g/cm³ × 175616 cm³

Calculating this gives:

Mass = 1843.968 grams

Since the question asks for the mass in kilograms, we convert grams to kilograms (1 kg = 1000 g):

Mass = 1843.968 g × (1 kg / 1000 g) = 1.843968 kg

Considering significant figures, the original measurement of 0.56 meters has 2 significant figures, while 10.5 has 3. Therefore, we round our final answer to 2 significant figures:

Mass ≈ 1.8 kg or 1800 kg

This example illustrates the importance of dimensional analysis and unit conversion in solving problems involving density and volume. By carefully managing units and significant figures, we can arrive at a precise and accurate answer.