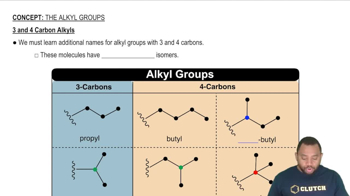
Here are the essential concepts you must grasp in order to answer the question correctly.
Carbon-14 Dating
Carbon-14 dating is a radiometric dating method used to determine the age of organic materials by measuring the amount of carbon-14 they contain. Living organisms absorb carbon-14 from the atmosphere, and when they die, the carbon-14 begins to decay at a known rate, characterized by its half-life. This technique is particularly useful for dating materials up to about 50,000 years old.
Recommended video:
Half-Life
The half-life of a radioactive isotope is the time required for half of the isotope in a sample to decay into a different element or isotope. For carbon-14, the half-life is approximately 5,715 years. Understanding half-life is crucial for calculating the age of a sample based on the remaining amount of carbon-14 compared to its initial concentration in living organisms.
Recommended video:
Disintegration Rate
The disintegration rate refers to the number of radioactive decays occurring per unit time, typically expressed in disintegrations per minute (dis/min). In this context, the disintegration rate of carbon-14 in living organisms is higher than in a deceased organism, allowing scientists to estimate the time since death by comparing the current decay rate to the known rate in living organisms.
Recommended video:

 Verified step by step guidance
Verified step by step guidance