Skip to main content
Pearson+ LogoPearson+ Logo
Ch.19 - Free Energy & Thermodynamics
All textbooksTro 6th EditionCh.19 - Free Energy & ThermodynamicsProblem 43a
Chapter 19, Problem 43a

Given the values of ΔH°rxn, ΔS°rxn, and T, determine ΔSuniv and predict whether or not each reaction is spontaneous. (Assume that all reactants and products are in their standard states.) a. ΔH°rxn = +135 kJ; ΔS°rxn = -282 J/K; T = 298 K

Verified step by step guidance
1
Identify the formula for the change in entropy of the universe: \( \Delta S_{univ} = \Delta S_{sys} + \Delta S_{surr} \).
Recognize that \( \Delta S_{sys} \) is given as \( \Delta S^{\circ}_{rxn} = -282 \text{ J/K} \).
Calculate \( \Delta S_{surr} \) using the formula \( \Delta S_{surr} = -\frac{\Delta H^{\circ}_{rxn}}{T} \). Convert \( \Delta H^{\circ}_{rxn} \) from kJ to J by multiplying by 1000.
Substitute the values into the formula: \( \Delta S_{surr} = -\frac{135,000 \text{ J}}{298 \text{ K}} \).
Add \( \Delta S_{sys} \) and \( \Delta S_{surr} \) to find \( \Delta S_{univ} \). If \( \Delta S_{univ} > 0 \), the reaction is spontaneous; if \( \Delta S_{univ} < 0 \), it is non-spontaneous.

Verified video answer for a similar problem:

This video solution was recommended by our tutors as helpful for the problem above.
Video duration:
4m
Was this helpful?

Key Concepts

Here are the essential concepts you must grasp in order to answer the question correctly.

Gibbs Free Energy

Gibbs Free Energy (G) is a thermodynamic potential that helps predict the spontaneity of a reaction at constant temperature and pressure. It is calculated using the equation ΔG = ΔH - TΔS, where ΔH is the change in enthalpy, T is the temperature in Kelvin, and ΔS is the change in entropy. A negative ΔG indicates a spontaneous reaction, while a positive ΔG suggests non-spontaneity.
Recommended video:
Guided course
01:51
Gibbs Free Energy of Reactions

Entropy (ΔS)

Entropy (ΔS) is a measure of the disorder or randomness in a system. In the context of chemical reactions, a positive change in entropy (ΔS > 0) typically favors spontaneity, as systems tend to evolve towards greater disorder. Conversely, a negative change in entropy (ΔS < 0) indicates a decrease in disorder, which can hinder spontaneity depending on the enthalpy change.
Recommended video:
Guided course
02:46
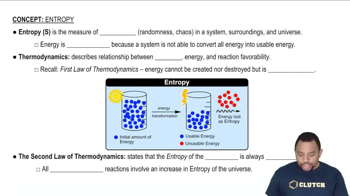
Entropy in Thermodynamics

Enthalpy (ΔH)

Enthalpy (ΔH) is a measure of the total heat content of a system and reflects the energy absorbed or released during a reaction. A positive ΔH indicates that the reaction is endothermic (absorbs heat), while a negative ΔH indicates an exothermic reaction (releases heat). The sign and magnitude of ΔH, in conjunction with ΔS, are crucial for determining the overall spontaneity of a reaction through the Gibbs Free Energy equation.
Recommended video:
Guided course
02:34
Enthalpy of Formation
Related Practice
Textbook Question

Without doing any calculations, determine the signs of ΔSsys and ΔS surr for each chemical reaction. In addition, predict under what temperatures (all temperatures, low temperatures, or high temperatures), if any, the reaction is spontaneous. a. C3H8(g) + 5 O2(g) → 3 CO2(g) + 4 H2O(g) ΔH°rxn = -2044 kJ

Textbook Question

Without doing any calculations, determine the signs of ΔSsys and ΔSsurr for each chemical reaction. In addition, predict under what temperatures (all temperatures, low temperatures, or high temperatures), if any, the reaction is spontaneous. c. C3H8(g) + 5 O2(g) → 3 CO2(g) + 4 H2O(g) ΔH°rxn = -2044 kJ

Textbook Question

Calculate ΔSsurr at the indicated temperature for each reaction. d. ΔH°rxn = +114 kJ; 77 K

Textbook Question

Given the values of ΔH°rxn, ΔS°rxn, and T, determine ΔSuniv and predict whether or not each reaction is spontaneous. (Assume that all reactants and products are in their standard states.) c. ΔH°rxn = -135 kJ; ΔS°rxn = -282 J>K; T = 298 K

Textbook Question

Given the values of ΔH°rxn, ΔS°rxn, and T, determine ΔSuniv and predict whether or not each reaction is spontaneous. (Assume that all reactants and products are in their standard states.) a. ΔH°rxn = -75 kJ; ΔS°rxn = -127 J/K; T = 298 K

Textbook Question

Given the values of ΔH°rxn, ΔS°rxn, and T, determine ΔSuniv and predict whether or not each reaction is spontaneous. (Assume that all reactants and products are in their standard states.) c. ΔH°rxn = +75 kJ; ΔS°rxn = -127 J/K; T = 298 K