Calculate the vapor pressure of a solution containing 38.3 g of glycerin (C3H8O3) in 135 mL of water at 30.0 °C. The vapor pressure of pure water at this temperature is 31.8 torr. Assume that glycerin is not volatile and dissolves molecularly (i.e., it is not ionic), and use a density of 1.00 g>mL for the water.

A solution contains 4.08 g of chloroform (CHCl3) and 9.29 g of acetone (CH3COCH3). The vapor pressures at 35 °C of pure chloroform and pure acetone are 295 torr and 332 torr, respectively. Assuming ideal behavior, calculate the vapor pressures of each of the components and the total vapor pressure above the solution. The experimentally measured total vapor pressure of the solution at 35 °C is 312 torr. Is the solution ideal? If not, what can you say about the relative strength of chloroform–acetone interactions compared to the acetone–acetone and chloroform–chloroform interactions?
 Verified step by step guidance
Verified step by step guidanceKey Concepts
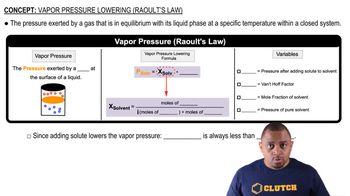
Raoult's Law
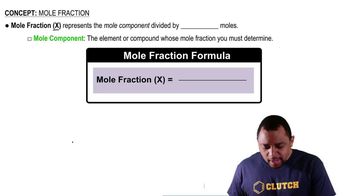
Mole Fraction
Ideal vs. Non-Ideal Solutions

A solution contains 50.0 g of heptane (C7H16) and 50.0 g of octane (C8H18) at 25 °C. The vapor pressures of pure heptane and pure octane at 25 °C are 45.8 torr and 10.9 torr, respectively. Assuming ideal behavior, answer the following: d. Why is the composition of the vapor different from the composition of the solution?
A solution contains a mixture of pentane and hexane at room temperature. The solution has a vapor pressure of 258 torr. Pure pentane and hexane have vapor pressures of 425 torr and 151 torr, respectively, at room temperature. What is the mole fraction composition of the mixture? (Assume ideal behavior.)
A glucose solution contains 74.2 g of glucose (C6H12O6) in 455 g of water. Determine the freezing point and boiling point of the solution.
