How many molecular orbitals are present in the conduction band of a sodium crystal with a mass of 3.67 g?

Verified step by step guidance

Determine the molar mass of sodium (Na), which is approximately 22.99 g/mol.

Calculate the number of moles of sodium in the given mass using the formula: \( \text{moles of Na} = \frac{\text{mass of Na}}{\text{molar mass of Na}} \).

Use Avogadro's number (\(6.022 \times 10^{23}\) atoms/mol) to find the total number of sodium atoms in the sample: \( \text{number of Na atoms} = \text{moles of Na} \times 6.022 \times 10^{23} \).

In a sodium crystal, each sodium atom contributes one electron to the conduction band. Therefore, the number of molecular orbitals in the conduction band is equal to the number of sodium atoms.

Conclude that the number of molecular orbitals in the conduction band is equal to the number of sodium atoms calculated in the previous step.

Verified video answer for a similar problem:

This video solution was recommended by our tutors as helpful for the problem above.

Video duration:

Was this helpful?

Key Concepts

Here are the essential concepts you must grasp in order to answer the question correctly.

Molecular Orbitals

Molecular orbitals are formed by the linear combination of atomic orbitals when atoms bond together. In a solid, such as a sodium crystal, these orbitals can extend over many atoms, leading to the formation of bands, including the conduction band, which allows for electron movement and conductivity.

Conduction Band

The conduction band is a range of energy levels in a solid where electrons can move freely, contributing to electrical conductivity. In metals like sodium, the conduction band is partially filled, allowing electrons to flow easily under an applied electric field, which is essential for the material's conductive properties.

Density of States

The density of states refers to the number of available electronic states at a given energy level in a solid. It is crucial for determining how many molecular orbitals are present in the conduction band, as it helps calculate the total number of states that electrons can occupy, influencing the material's electrical and thermal properties.

Recommended video:

Guided course

01:56

Density Concepts

Related Practice

Textbook Question

Which solid would you expect to have little or no band gap? a. Cu(s) b. Si(s) c. As(s)

Textbook Question

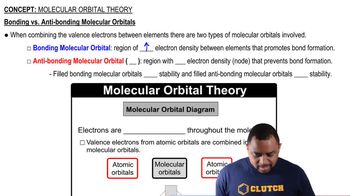
Which solid would you expect to have the largest band gap? a. As(s) b. Sb(s) c. Bi(s)

Textbook Question

A substance has a band gap of 5.8 eV at 273 K. Is this substance best classified as an insulator, a semiconductor, or a metal?

Textbook Question

Indicate if each solid forms an n-type or a p-type semiconductor. b. germanium doped with gallium

Textbook Question

Does a photon of red light with a frequency of 4.29⨉10¹⁴ Hz have sufficient energy to promote an electron from the valence band to the conduction band in a sample of silicon (the band gap in silicon is 1.11 eV)?