The energy required to ionize sodium is 496 kJ/mol. What minimum frequency of light is required to ionize sodium?
Ch.8 - The Quantum-Mechanical Model of the Atom

Chapter 8, Problem 83
An atomic emission spectrum of hydrogen shows three wavelengths: 1875 nm, 1282 nm, and 1093 nm. Assign these wavelengths to transitions in the hydrogen atom.
 Verified step by step guidance
Verified step by step guidance1
Identify the series of transitions in the hydrogen atom: Lyman, Balmer, and Paschen series.
Recall that the Lyman series involves transitions to the n=1 level, the Balmer series to the n=2 level, and the Paschen series to the n=3 level.
Convert the given wavelengths from nanometers to meters for calculation purposes.
Use the Rydberg formula \( \frac{1}{\lambda} = R_H \left( \frac{1}{n_1^2} - \frac{1}{n_2^2} \right) \) to calculate the initial and final energy levels (n1 and n2) for each wavelength.
Assign each wavelength to the appropriate series based on the calculated energy levels and the known series transitions.

Verified video answer for a similar problem:
This video solution was recommended by our tutors as helpful for the problem above.
Video duration:
15mWas this helpful?
Key Concepts
Here are the essential concepts you must grasp in order to answer the question correctly.
Atomic Emission Spectrum
An atomic emission spectrum is a spectrum of the electromagnetic radiation emitted by a substance when its atoms transition from a higher energy state to a lower energy state. Each element has a unique emission spectrum, which can be used to identify the element and understand its electronic structure. The wavelengths observed correspond to specific energy differences between electron orbits in the atom.
Recommended video:
Guided course

Atomic Emission Spectra
Energy Levels in Hydrogen Atom
In a hydrogen atom, electrons occupy discrete energy levels, which are quantized. When an electron transitions between these levels, it either absorbs or emits a photon with energy equal to the difference between the two levels. The energy levels can be calculated using the Rydberg formula, which helps in determining the wavelengths of light emitted during these transitions.
Recommended video:
Guided course
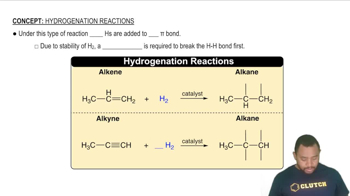
Hydrogenation Reactions
Rydberg Formula
The Rydberg formula is a mathematical equation used to predict the wavelengths of spectral lines in hydrogen and other hydrogen-like atoms. It is expressed as 1/λ = R_H (1/n1² - 1/n2²), where λ is the wavelength, R_H is the Rydberg constant, and n1 and n2 are the principal quantum numbers of the lower and higher energy levels, respectively. This formula is essential for assigning observed wavelengths to specific electronic transitions.
Recommended video:
Guided course
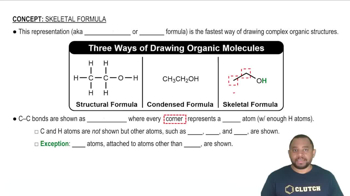
Skeletal Formula
Related Practice
Textbook Question
Textbook Question
Suppose that in an alternate universe, the possible values of l are the integer values from 0 to n (instead of 0 to n - 1). Assuming no other differences between this imaginary universe and ours, how many orbitals would exist in each level? a. n = 1 b. n = 2 c. n = 3
Textbook Question
Suppose that, in an alternate universe, the possible values of ml are the integer values including 0 ranging from -l -1 to l +1 (instead of simply -l to +l). How many orbitals exist in each sublevel? a. s sublevel b. p sublevel c. d sublevel
Textbook Question
An atomic emission spectrum of hydrogen shows three wavelengths: 121.5 nm, 102.6 nm, and 97.23 nm. Assign these wavelengths to transitions in the hydrogen atom.
