Neutron stars are composed of solid nuclear matter, primarily neutrons. Assume the radius of a neutron is approximately 1.0×10–13 cm. Calculate the density of a neutron. [Hint: For a sphere V = (4/3)πr3.] Assuming that a neutron star has the same density as a neutron, calculate the mass (in kg) of a small piece of a neutron star the size of a spherical pebble with a radius of 0.10 mm.

Carbon-12 contains six protons and six neutrons. The radius of the nucleus is approximately 2.7 fm (femtometers) and the radius of the atom is approximately 70 pm (picometers). Calculate the volume of the nucleus and the volume of the atom.
 Verified step by step guidance
Verified step by step guidance
Verified video answer for a similar problem:
Key Concepts
Nuclear Volume Calculation

Atomic Volume Calculation
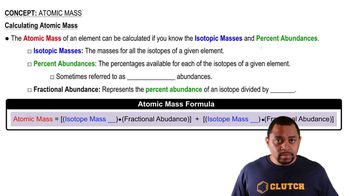
Unit Conversion

Carbon-12 contains six protons and six neutrons. The radius of the nucleus is approximately 2.7 fm (femtometers) and the radius of the atom is approximately 70 pm (picometers). What percentage of the carbon atom's volume is occupied by the nucleus? (Assume two significant figures.)
A penny has a thickness of approximately 1.0 mm. If you stacked Avogadro's number of pennies one on top of the other on Earth's surface, how far would the stack extend (in km)? [For comparison, the sun is about 150 million km from Earth and the nearest star (Proxima Centauri) is about 40 trillion km from Earth.]
Consider the stack of pennies in the previous problem. How much money (in dollars) would this represent? If this money were equally distributed among the world's population of 7.0 billion people, how much would each person receive? Would each person be a millionaire? A billionaire? A trillionaire?
