The half-life for the radioactive decay of C-14 is 5730 years and is independent of the initial concentration. If a sample of C-14 initially contains 1.5 mmol of C-14, how many millimoles are left after 2255 years?

Verified step by step guidance

Step 1: Understand the concept of half-life. The half-life of a radioactive substance is the time it takes for half of the substance to decay. In this case, the half-life of C-14 is 5730 years, which means that after 5730 years, half of the initial amount of C-14 will have decayed.

Step 2: Calculate the number of half-lives that have passed. This can be done by dividing the total time that has passed (2255 years) by the half-life of the substance (5730 years).

Step 3: Use the formula for exponential decay to calculate the remaining amount of C-14. The formula is N = N0 * (1/2)^(t/t_half), where N is the final amount, N0 is the initial amount, t is the time that has passed, and t_half is the half-life.

Step 4: Substitute the given values into the formula. N0 is the initial amount of C-14, which is 1.5 mmol. t is the time that has passed, which is 2255 years. t_half is the half-life of C-14, which is 5730 years.

Step 5: Solve the equation to find the remaining amount of C-14. This will give you the amount of C-14 that is left after 2255 years.

Verified video answer for a similar problem:

This video solution was recommended by our tutors as helpful for the problem above.

Video duration:

Was this helpful?

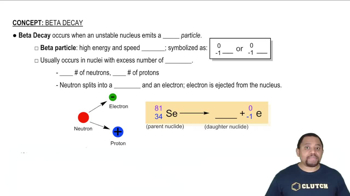
Key Concepts

Here are the essential concepts you must grasp in order to answer the question correctly.

Half-life

Half-life is the time required for half of the radioactive nuclei in a sample to decay. For C-14, this period is 5730 years, meaning that after this time, only half of the original amount remains. Understanding half-life is crucial for calculating the remaining quantity of a radioactive substance after a specific time has elapsed.

Exponential decay

Exponential decay describes the process by which a quantity decreases at a rate proportional to its current value. In the context of radioactive decay, the amount of C-14 decreases exponentially over time, which can be mathematically represented by the equation N(t) = N0 * (1/2)^(t/T), where N0 is the initial amount, t is the elapsed time, and T is the half-life.

Radioactive decay formula

The radioactive decay formula allows us to calculate the remaining quantity of a radioactive isotope after a certain period. For C-14, the formula can be applied to determine how much remains after 2255 years by substituting the values into the exponential decay equation, taking into account the half-life of 5730 years to find the remaining millimoles.

Recommended video:

Guided course

03:00

Rate of Radioactive Decay

Related Practice

Textbook Question

The half-life for the radioactive decay of U-238 is 4.5 billion years and is independent of initial concentration. How long will it take for 10% of the U-238 atoms in a sample of U-238 to decay?

views

Textbook Question

The half-life for the radioactive decay of U-238 is 4.5 billion years and is independent of initial concentration. If a sample of U-238 initially contained 1.5⨉10¹⁸ atoms when the universe was formed 13.8 billion years ago, how many U-238 atoms does it contain today?

Textbook Question

The half-life for the radioactive decay of C-14 is 5730 years and is independent of the initial concentration. How long does it take for 25% of the C-14 atoms in a sample of C-14 to decay?

Textbook Question

The diagram shows the energy of a reaction as the reaction progresses. Label each blank box in the diagram.

a. reactants b. products c. activation energy (E_a) d. enthalpy of reaction (ΔH_rxn)

Textbook Question

The activation energy of a reaction is 56.8 kJ/mol and the frequency factor is 1.5⨉10¹¹/ s. Calculate the rate constant of the reaction at 25 °C.

Textbook Question

The rate constant (k) for a reaction was measured as a function of temperature. A plot of ln k versus 1/T (in K) is linear and has a slope of -7445 K. Calculate the activation energy for the reaction.

views