The desorption (leaving of the surface) of a single molecular layer of n-butane from a single crystal of aluminum oxide is found to be first order with a rate constant of 0.128 s−1 at 150 K. If the surface is initially completely covered, what fraction will remain covered after 10 s? After 20 s?

Verified step by step guidance

Identify that the desorption process follows first-order kinetics, which can be described by the equation: \( [A] = [A]_0 e^{-kt} \), where \([A]\) is the concentration at time \(t\), \([A]_0\) is the initial concentration, \(k\) is the rate constant, and \(t\) is the time.

Recognize that the problem asks for the fraction of the surface that remains covered, which corresponds to \( \frac{[A]}{[A]_0} \).

Substitute the given rate constant \(k = 0.128 \text{ s}^{-1}\) and the time \(t = 10 \text{ s}\) into the first-order kinetics equation to find the fraction remaining after 10 seconds: \( \frac{[A]}{[A]_0} = e^{-0.128 \times 10} \).

Repeat the substitution for \(t = 20 \text{ s}\) to find the fraction remaining after 20 seconds: \( \frac{[A]}{[A]_0} = e^{-0.128 \times 20} \).

Interpret the results: the calculated values from the equations will give you the fraction of the surface that remains covered after 10 seconds and 20 seconds, respectively.

Key Concepts

Here are the essential concepts you must grasp in order to answer the question correctly.

First-Order Kinetics

First-order kinetics refers to a reaction rate that is directly proportional to the concentration of one reactant. In this case, the desorption of n-butane follows first-order kinetics, meaning the rate of desorption decreases exponentially as the concentration of n-butane on the surface decreases. The mathematical representation is given by the equation: ln([A]0/[A]) = kt, where [A]0 is the initial concentration, [A] is the concentration at time t, k is the rate constant, and t is time.

Exponential Decay

Exponential decay describes the process by which a quantity decreases at a rate proportional to its current value. In the context of this question, the fraction of n-butane remaining on the surface decreases exponentially over time due to the first-order desorption process. This can be expressed mathematically as [A] = [A]0 e^(-kt), where e is the base of the natural logarithm, indicating how the concentration diminishes over time.

Fraction Remaining

The fraction remaining refers to the proportion of a substance that is still present after a certain period. To calculate the fraction of n-butane remaining on the aluminum oxide surface after specific time intervals, one can use the first-order kinetics equation. By substituting the values of k and t into the equation, one can determine how much of the initial coverage remains after 10 seconds and 20 seconds, providing insight into the desorption process.

Recommended video:

Guided course

00:36

Mole Fraction Formula

Related Practice

Textbook Question

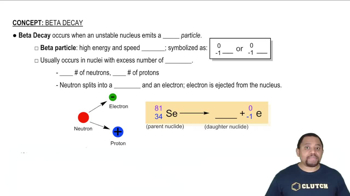
Consider the reaction in which HCl adds across the double bond of ethene: HCl + H₂C=CH₂ → H₃C-CH₂Cl The following mechanism, with the accompanying energy diagram, has been suggested for this reaction:

Step 1 HCl + H₂C=CH₂ → H₃C=CH₂⁺ + Cl^-

Step 2 H₃C=CH₂⁺ + Cl^- → H₃C-CH₂Cl

a. Based on the energy diagram, determine which step is rate limiting.

Textbook Question

Step 1 HCl + H₂C=CH₂ → H₃C=CH₂⁺ + Cl^-

Step 2 H₃C=CH₂⁺ + Cl^- → H₃C-CH₂Cl

b. What is the expected order of the reaction based on the proposed mechanism?

Textbook Question

The desorption (leaving of the surface) of a single molecular layer of n-butane from a single crystal of aluminum oxide is found to be first order with a rate constant of 0.128/s at 150 K. b. If the surface is initially completely covered with n-butane at 150 K, how long will it take for 25% of the molecules to desorb (leave the surface)? For 50% to desorb?