Lead metal can be extracted from a mineral called galena, which contains 86.6% lead by mass. A particular ore contains 68.5% galena by mass. If the lead can be extracted with 92.5% efficiency, what mass of ore is required to make a lead sphere with a 5.00-cm radius?
Verified step by step guidance
1
Calculate the volume of the lead sphere using the formula for the volume of a sphere: $V = \frac{4}{3} \pi r^3$, where $r$ is the radius of the sphere.
Determine the mass of the lead sphere using the density of lead, which is approximately 11.34 g/cm³. Use the formula: $\text{mass} = \text{density} \times \text{volume}$.
Calculate the mass of lead required from the ore, considering the extraction efficiency. Use the formula: $\text{mass of lead required} = \frac{\text{mass of lead sphere}}{\text{extraction efficiency}}$.
Determine the mass of galena needed to obtain the required mass of lead. Use the formula: $\text{mass of galena} = \frac{\text{mass of lead required}}{\text{percentage of lead in galena}}$.
Calculate the mass of ore needed to provide the required mass of galena. Use the formula: $\text{mass of ore} = \frac{\text{mass of galena}}{\text{percentage of galena in ore}}$.
Verified video answer for a similar problem:
This video solution was recommended by our tutors as helpful for the problem above.
Video duration:
3m
Play a video:
Was this helpful?
Key Concepts
Here are the essential concepts you must grasp in order to answer the question correctly.
Mass Percent Composition
Mass percent composition refers to the percentage by mass of a specific element or compound in a mixture or compound. In this question, understanding that galena contains 86.6% lead by mass is crucial for calculating the amount of lead available in the ore. This concept allows us to determine how much lead can be extracted from a given mass of galena.
The volume of a sphere is calculated using the formula V = (4/3)πr³, where r is the radius. In this problem, the radius of the lead sphere is given as 5.00 cm, and calculating its volume is essential to determine the total mass of lead needed. This mass will then be used to backtrack to the required mass of ore.
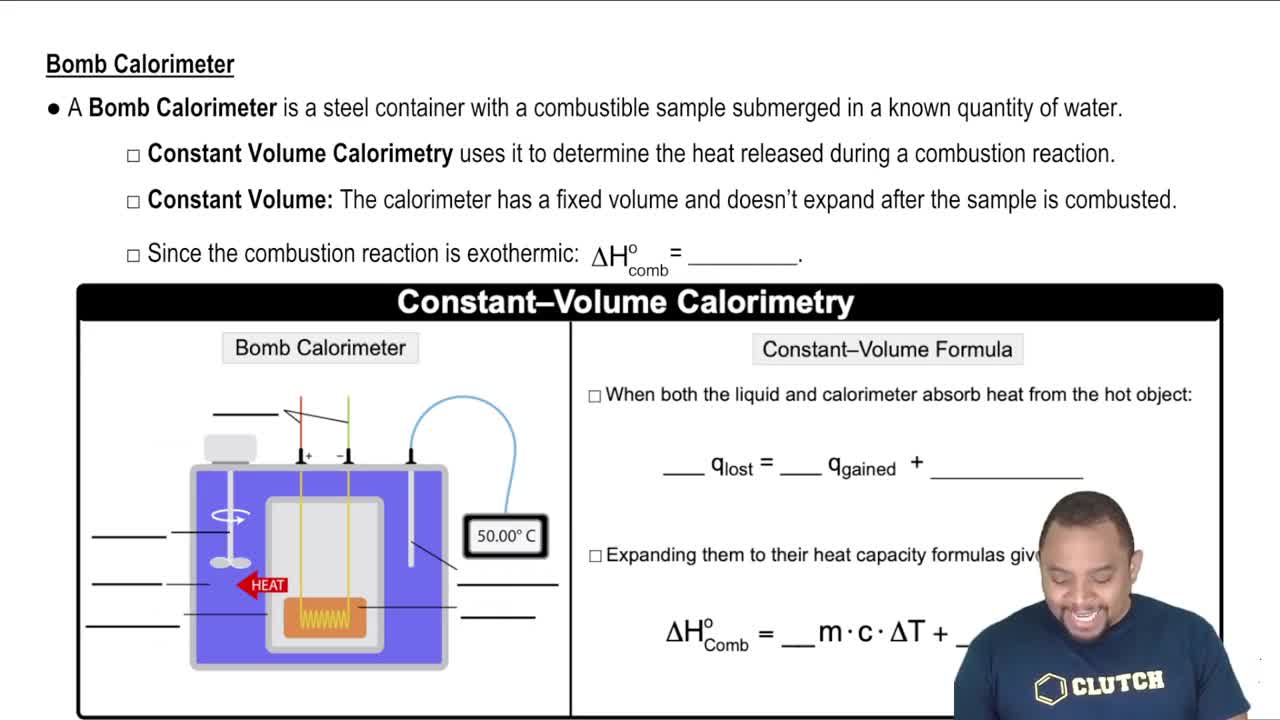
Extraction efficiency is the percentage of the total amount of a substance that can be successfully extracted from a source material. In this case, the lead can be extracted with 92.5% efficiency, meaning that not all the lead present in the galena will be recovered. This concept is vital for adjusting the calculations to account for losses during the extraction process, ensuring accurate determination of the ore mass needed.
Verified step by step guidance
00:38
