Sketch the 3d orbitals. How do the 4d orbitals differ from the 3d orbitals?

According to the quantum-mechanical model for the hydrogen atom, which electron transition produces light with the longer wavelength: 2p to 1s or 3p to 1s?
 Verified step by step guidance
Verified step by step guidanceKey Concepts
Quantum Mechanical Model

Electron Transitions
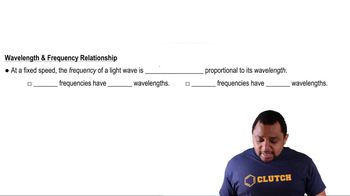
Wavelength and Energy Relationship
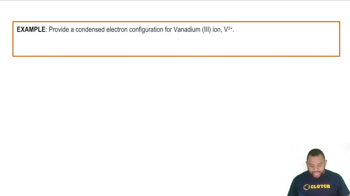
Determine whether each transition in the hydrogen atom corresponds to absorption or emission of energy. a. n = 3 → n = 1 b. n = 2 → n = 4 c. n = 4 → n = 3
According to the quantum-mechanical model for the hydrogen atom, which electron transition produces light with the longer wavelength: 3p → 2s or 4p → 3p?
Calculate the wavelength of the light emitted when an electron in a hydrogen atom makes each transition and indicate the region of the electromagnetic spectrum (infrared, visible, ultraviolet, etc.) where the light is found. a. n = 2 → n = 1 b. n = 3 → n = 1 c. n = 4 → n = 2 d. n = 5 → n = 2
Calculate the frequency of the light emitted when an electron in a hydrogen atom makes each transition: a. n = 4 → n = 3 b. n = 5 → n = 1 c. n = 5 → n = 4 d. n = 6 → n = 5
