Calculate the quantity of energy produced per gram of U-235 (atomic mass = 235.043922 amu) for the neutron-induced fission of U-235 to form Xe-144 (atomic mass = 143.9385 amu) and Sr-90 (atomic mass = 89.907738 amu) (discussed in Problem 57).
Ch.20 - Radioactivity and Nuclear Chemistry

Chapter 20, Problem 72
Calculate the quantity of energy produced per gram of reactant for the fusion of H-3 (atomic mass = 3.016049 amu) with H-1 (atomic mass = 1.007825 amu) to form He-4 (atomic mass = 4.002603 amu).
 Verified step by step guidance
Verified step by step guidance1
Identify the nuclear reaction: \( \text{H-3} + \text{H-1} \rightarrow \text{He-4} \).
Calculate the mass defect: \( \Delta m = (\text{mass of H-3} + \text{mass of H-1}) - \text{mass of He-4} \).
Convert the mass defect from atomic mass units (amu) to kilograms using the conversion factor: 1 amu = 1.66053906660 \times 10^{-27} \text{ kg}.
Use Einstein's equation \( E = \Delta m c^2 \) to calculate the energy released, where \( c \) is the speed of light \( 3.00 \times 10^8 \text{ m/s} \).
Calculate the energy produced per gram of reactant by dividing the total energy by the total mass of the reactants in grams.
Key Concepts
Here are the essential concepts you must grasp in order to answer the question correctly.
Nuclear Fusion
Nuclear fusion is a process where two light atomic nuclei combine to form a heavier nucleus, releasing energy in the process. This reaction is the source of energy for stars, including the sun, and occurs under extreme temperature and pressure conditions. In the given question, the fusion of H-3 and H-1 to form He-4 exemplifies this process.
Recommended video:
Guided course

Nuclear Binding Energy
Mass-Energy Equivalence
Mass-energy equivalence, encapsulated in Einstein's equation E=mc², states that mass can be converted into energy and vice versa. In nuclear reactions, the mass of the reactants is often greater than the mass of the products, with the 'missing' mass converted into energy. This principle is crucial for calculating the energy produced in the fusion reaction described.
Recommended video:
Guided course
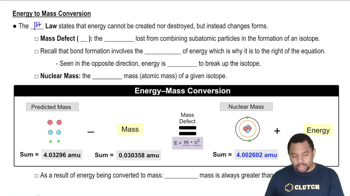
Energy to Mass Conversion
Binding Energy
Binding energy is the energy required to disassemble a nucleus into its constituent protons and neutrons. It reflects the stability of a nucleus; higher binding energy indicates a more stable nucleus. In fusion reactions, the difference in binding energy between the reactants and products determines the energy released, which is essential for solving the energy calculation in the question.
Recommended video:
Guided course

Nuclear Binding Energy
Related Practice
Textbook Question
Textbook Question
Calculate the quantity of energy produced per mole of U-235 (atomic mass = 235.043922 amu) for the neutron-induced fission of U-235 to produce Te-137 (atomic mass = 136.9253 amu) and Zr-97 (atomic mass = 96.910950 amu) (discussed in Problem 58).
Textbook Question
A 75-kg human has a dose of 32.8 rad of radiation. How much energy is absorbed by the person's body? Compare this energy to the amount of energy absorbed by the person's body if he or she jumped from a chair to the floor (assume that the chair is 0.50 m from the ground and that all of the energy from the fall is absorbed by the person).
1
views
